Equal weights of Zn metal and iodine are mixed together and I1 is completley converted to ZnI2. What fractionn by weight of original Zn remains unreacted? (Zn=65,I=127)
0.34
0.74
0.84
Unable to predict
The correct Answer is:B
To solve the problem, we need to determine the fraction by weight of the original zinc (Zn) that remains unreacted after it reacts with iodine (I2) to form zinc iodide (ZnI2).
1. Write the Balanced Chemical Equation:
The reaction between zinc and iodine can be represented as:
Zn+I2→ZnI2
2. Assume Equal Weights:
Let the weight of zinc (Zn) and iodine (I2) taken initially be W grams each.
3. Calculate Moles of Zinc and Iodine:
- Moles of zinc:
Moles of Zn=W65
- Moles of iodine (I2):
Moles of I2=W254
(Note: The molar mass of I2 is 127×2=254 g/mol)
4. Identify the Limiting Reagent:
The balanced equation shows that zinc and iodine react in a 1:1 ratio. Therefore, we compare the moles:
- Moles of Zn = W65
- Moles of I2 = W254
Since W254<W65, iodine (I2) is the limiting reagent and will be completely consumed.
5. Calculate Moles of Zinc Remaining:
The moles of zinc that react will be equal to the moles of iodine:
Moles of Zn reacted=W254
Therefore, the moles of zinc remaining will be:
Moles of Zn remaining=W65−W254
6. Calculate the Weight of Zinc Remaining:
The weight of zinc remaining can be calculated as:
Weight of Zn remaining=(W65−W254)×65
7. Calculate the Fraction of Zinc Remaining:
The fraction of the original weight of zinc that remains unreacted is given by:
Fraction of Zn remaining=Weight of Zn remainingW
Substituting the expression for weight of Zn remaining:
Fraction of Zn remaining=(W65−W254)×65W
8. Simplify the Expression:
Simplifying the fraction:
=165−1254
=254−6565×254=18916510
Now, calculating the fraction:
=18916510≈0.74
Final Answer:
The fraction by weight of the original zinc that remains unreacted is approximately 0.74.
The reaction between zinc and iodine can be represented as:
Zn+I2→ZnI2
Let the weight of zinc (Zn) and iodine (I2) taken initially be W grams each.
- Moles of zinc:
Moles of Zn=W65
- Moles of iodine (I2):
Moles of I2=W254
(Note: The molar mass of I2 is 127×2=254 g/mol)
The balanced equation shows that zinc and iodine react in a 1:1 ratio. Therefore, we compare the moles:
- Moles of Zn = W65
- Moles of I2 = W254
The moles of zinc that react will be equal to the moles of iodine:
Moles of Zn reacted=W254
Therefore, the moles of zinc remaining will be:
Moles of Zn remaining=W65−W254
The weight of zinc remaining can be calculated as:
Weight of Zn remaining=(W65−W254)×65
The fraction of the original weight of zinc that remains unreacted is given by:
Fraction of Zn remaining=Weight of Zn remainingW
Substituting the expression for weight of Zn remaining:
Fraction of Zn remaining=(W65−W254)×65W
Simplifying the fraction:
=165−1254
=254−6565×254=18916510
Now, calculating the fraction:
=18916510≈0.74
The fraction by weight of the original zinc that remains unreacted is approximately 0.74.
Topper's Solved these Questions
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - Level - 2
65 Videos
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - JEE Main (Archive)
33 Videos
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - Level -0 (Long Answer Type)
7 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-I
10 Videos
- STOICHIOMETRY-IIBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)
43 Videos
Similar Questions
If the atomic weight of Zn in 70 and its atomic number in 30, Then what be the atomic weight of Zn2+?
View SolutionAn open container has dimensions of 4.0m×5.0m and height of 3.0 m.
(i) Find the weight of the air in the container at 20∘C.
(ii) What is the weight of an equal volume of water ? Also find pressure at the base of container due to this weight pof water.
(iii) What is the total downward force on the base of the container due to air pressure of 1.0 atm ?
Take the denities of air and water as 1.2kg/m3 and 103kg/m3 respectively.
View Solution1.67 g mixture of Al and Zn was completely dissolved in acid and evolved 1.69 L of H2 at STP. Calculate the weight Al and Zn in the mixture.
View Solution(a) Explain the following terms :
(i) Rate of a reaction
(ii) Activation energy of a reaction
(b) The decompositon of phosphine , PH3, proceeds according to the following equation :
4PH3(g)→P4(g)+6H2(g)
It is found that the reaction follows the following rate equation :
Rate = k [PH3].
The half-life of PH3 is 37.9 s at 120∘C.
(i) How much time is required for 3/4thof PH3 to decompose ?
(ii) What fraction of the original sample of PH3 remains behind after 1 minute ?
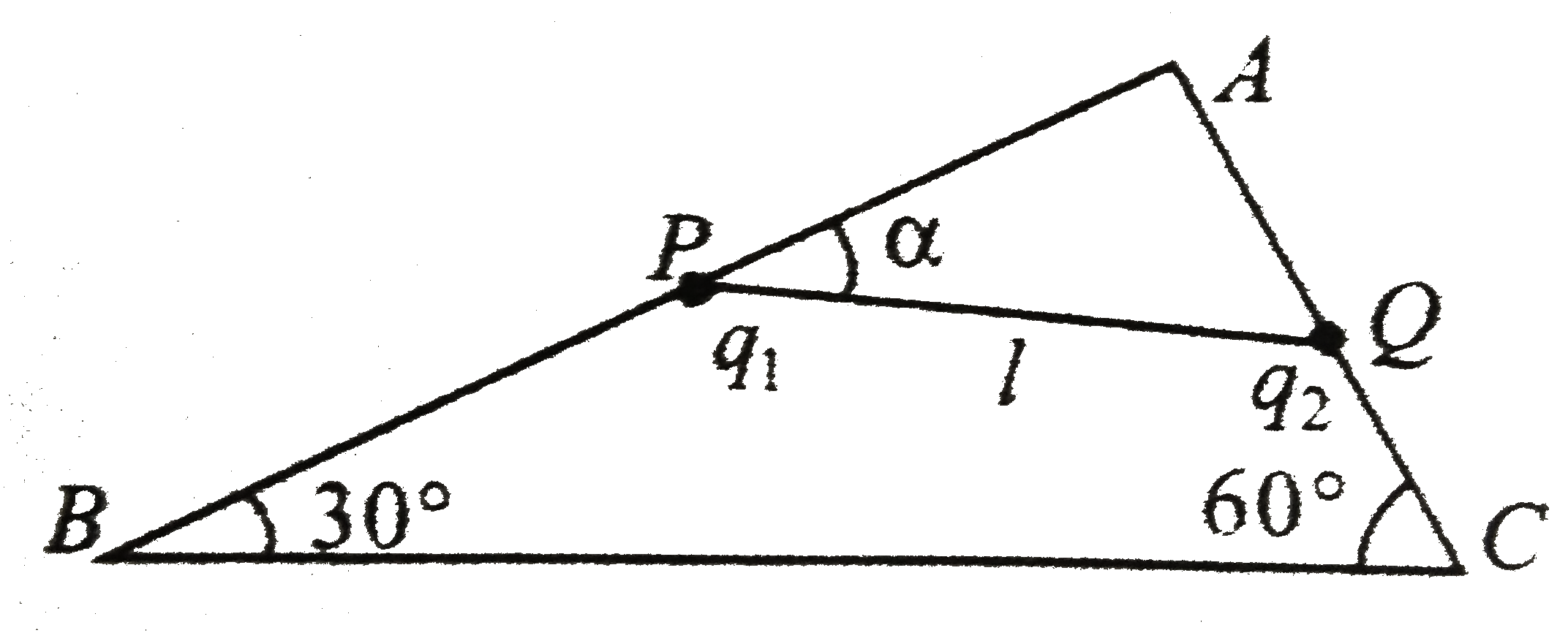
View SolutionA rigid insulated wire frame in the form of a right-angled triangle ABC is set in a vertical plane as shown in fig. two beads of equal masses m each and carrying charges q1 and q2 are connected by a cord of length l and can slide without friction on the wires.
Cinsidering the case when the beads are stationary, determine
(i) the angel α
(ii) the tension in the cord, and
(iii) The normal recation on teh beads.
If the cord is now cut, what are the value of the charges for which the beads continue to remain stationary?
View SolutionA 200W, 110 V incadescent lamp was connected with an electrolytic cell containing ZnCl2 . What weight of metal will be deposited on passing current for 1 hour? (At. Wt. of Zn=65.4)
View Solution
A true balance is one whose pans are of equal masses and arms are of equal lengths. When this happens, the net moment of forces about point of suspension is zero and beam remains horizontal without any weight i.e., for the true balance P1=P2 and l1=l2 also P1l1=P2l2 (mass of beam is neglibigle). A shopkeeper uses a false balance to weigh articles. Both arms and pans of this false balance are different, but beam become horizontal without any weight. (P1≠P2 and l1≠l2 but P1l1=P2l2).
Q. Shopkeeper use a weight W to weigh and article by false balance. in two weighing by using alternating pans let W1 and W2 are the weights of the article given to the customer i.e., customer gets (W1+W2) weight of article. Loss of gain to the shopkeeper is:
View SolutionIf 10g of V2O5 is dissolved in acid and is reduced to V2+ by zinc metal, how many mole I2 could be reduced by the resulting solution if it is further oxidised to VO2+ ions? [Assume no change in state of Zn2+ ions] (V=51, O=16, I=127)
View SolutionA solution containing both Zn2+ and Mn2+ ions at a concentration of 0.01M is saturated with H2S. What is pH at which MnS will form a ppt ? Under these conditions what will be the concentration of Zn2+ ions remaining in the solution ? Given Ksp of ZnSis10−22 and Ksp of MnS is 5.6×10−16,K1×K2 of H2S=1.10×10−21.
View SolutionTwo ampere current is passed through a solution of Zn+2 for 6 hours using steel cathode. Calculate the weight of zinc that can be plated on the cathode. If the cathode has a surface of 1/m2 and the radius of zinc atom is 0.625Å. What is the thickness of coating layer?
View Solution
