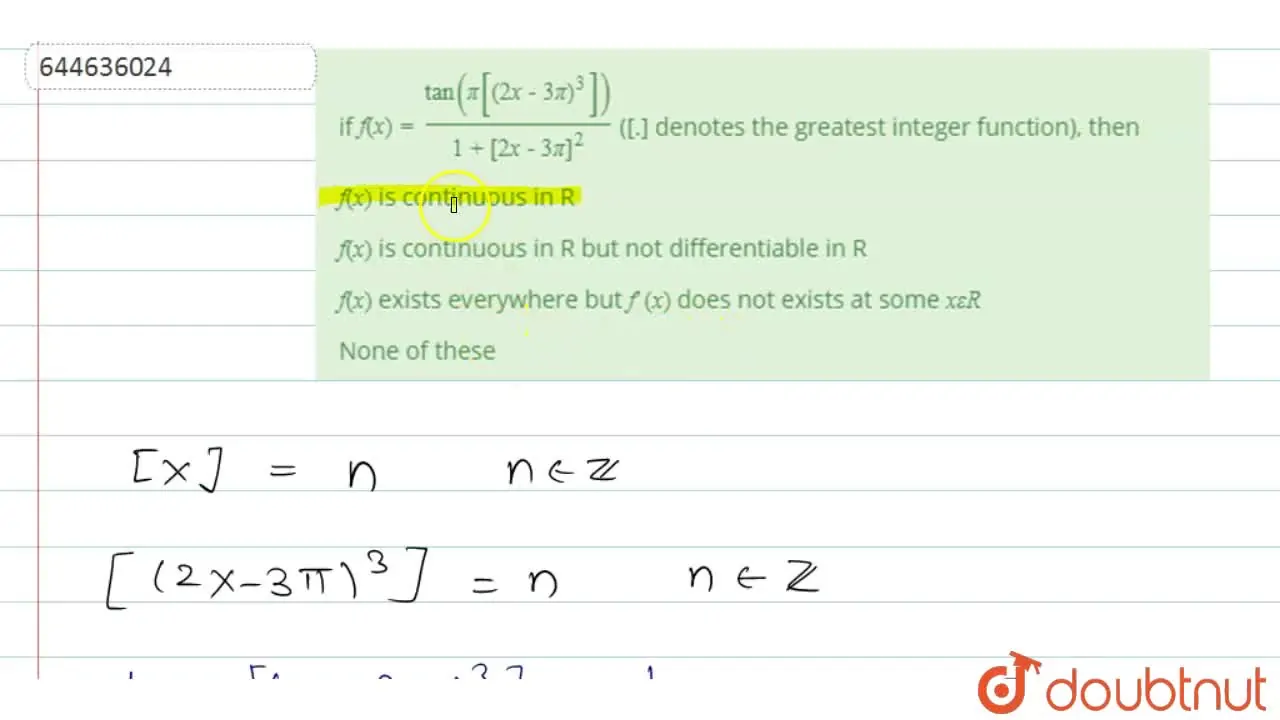
if f(x)=tan(π[(2x−3π)3])1+[2x−3π]2 ([.] denotes the greatest integer function), then
f(x) is continuous in R
f(x) is continuous in R but not differentiable in R
f(x) exists everywhere but f'(x) does not exists at some xεR
None of these
The correct Answer is:A
Step by step video & image solution for if f(x) = tan(pi[(2x-3pi)^3])/(1+[2x-3pi]^2) ([.] denotes the greatest integer function), then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - LEVEL 2103videos
DIFFERENTIAL CALCULUS
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - Numerical Value Type for JEE Main14videos
DIFFERENTIAL CALCULUS
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)75videos
DIFFERENTIAL CALCULUS
- BOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE76videos
CONIC SECTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)81videos
DIFFERENTIAL CALCULUS 2
Similar Questions
Let f(x)=sin(π[x−π])1+[x2] where [] denotes the greatest integer function then f(x) is
View SolutionLet f(x)=sin(π[x+π])1+[x]2 where [] denotes the greatest integer function then f(x) is
View SolutionLet f(x)=x(sinx+tanx)[x+ππ]−1/2 (where (.] denotes the greatest integer function) then find f(0).
View SolutionIf f(x)=sin([x]π)x2+x+1 , where [.] denotes the greatest integer function, then
View SolutionIf f(x)=sin{π2[x]−x5},1<x<2 and [.] denotes the greatest integer function, then f'(5√π2) is equal to
View SolutionIf f(x)=cos[π22]x+sin[−π22]x,[x] denoting the greatest integer function,then
View SolutionLet f(x)=sin{π[x−π]}1+[x2], where [.] stands for the greatest integer function. Then, f(x) is continuous or not?
View SolutionIf f:R→[−1,1] where f(x)=sin(π2[x]), (where [.] denotes the greatest integer fucntion), then
View SolutionIf [sinx]+[x2π]+[2x5π]=9x10π, where [⋅] denotes the greatest integer function, the number of solutions in the interval (30,40) is ………… .
View SolutionThe function f(x)=tan|π[x−π]|1+[x]2, where [x] denotes the greatest integer less than or equal to x, is
View Solution