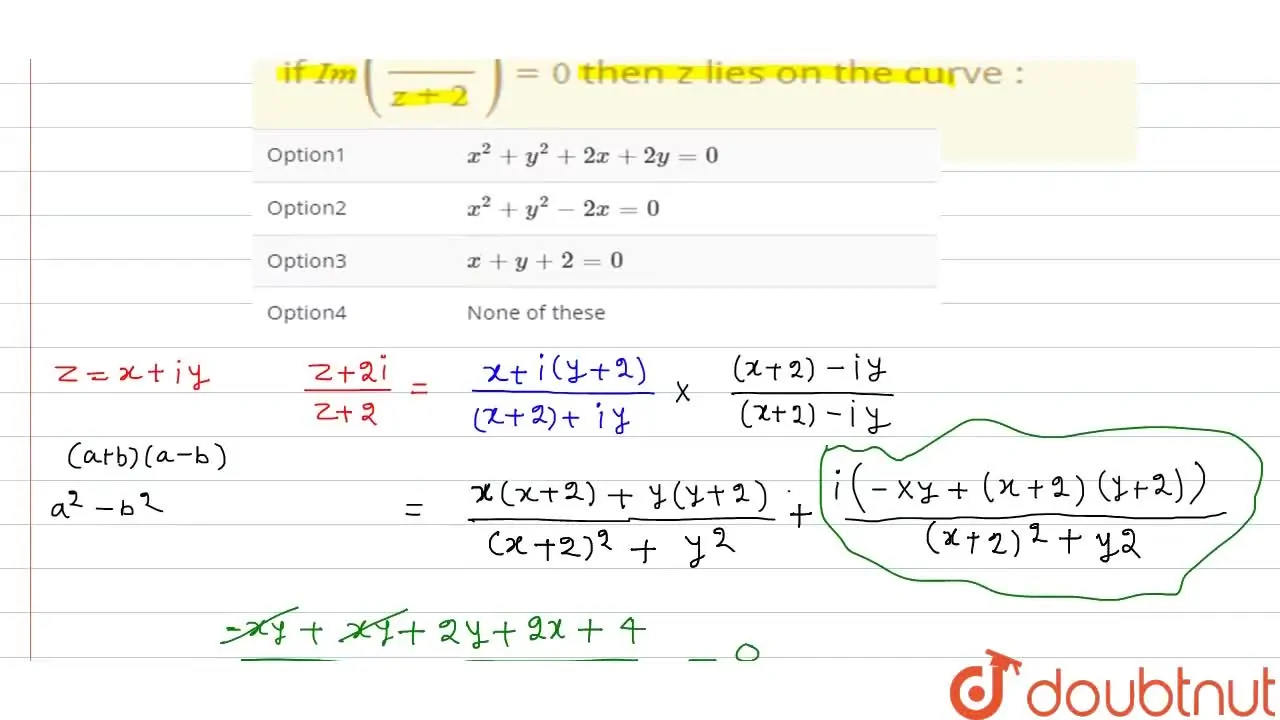
if Im(z+2iz+2)=0 then z lies on the curve :
x2+y2+2x+2y=0
x2+y2−2x=0
x+y+2=0
None of these
The correct Answer is:C
Step by step video & image solution for if Im((z+2i)/(z+2))= 0 then z lies on the curve : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - LEVEL - 250videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - NUMRICAL VALUE TYPE FOR JEE MAIN14videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - JEE ARCHIVE76videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - JEE ADVANCED ( ARCHIVE )68videos
CIRCLES
- BOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE76videos
CONIC SECTIONS
Similar Questions
If Re(z−8iz+6)=0, then z lies on the curve
View SolutionIf Re(z+2iz+4)=0 then z lies on a circle with centre :
View SolutionIf Im2z+1iz+1=−2, then locus of z, is
View SolutionIf |3z-1|=3|z-2|, then z lies on
View SolutionIf |z−iRe(z)|=|z−Im(z)| , then prove that z , lies on the bisectors of the quadrants.
View SolutionIf |z−iRe(z)|=|z−Im(z)| , then prove that z , lies on the bisectors of the quadrants.
View SolutionIf ∣∣∣z−iz+2i∣∣∣=1,|z|=52 then the value of |z+3i|
View SolutionIf ∣∣∣z−iz+2i∣∣∣=1,|z|=52 then the value of |z+3i|
View SolutionIf |z+¯z|+|z−¯z|=2, then z lies on
View SolutionIf Im(iz+2z+i)=−1 represents part of a circle with radius r units, then the value of 4r2 is (where, z∈C,z≠i,lm(z) represents the imaginary part of z and i2=−1)
View Solution