In a 3D hexagonal unit cell of identical atoms, the number of atoms that will contribute their 100% volume within the cell would be:
The correct Answer is:0
To determine the number of atoms that contribute their 100% volume within a hexagonal unit cell, we can follow these steps:
Step 1: Understand the Structure of the Hexagonal Unit Cell
The hexagonal unit cell is characterized by its unique arrangement of atoms. It is often referred to as the hexagonal close-packed (HCP) structure. In this structure, atoms are arranged in a way that maximizes packing efficiency.
Hint: Visualize the hexagonal unit cell and note the arrangement of atoms within it.
Step 2: Identify the Atoms in the Unit Cell
In a hexagonal unit cell, there are typically atoms located at the corners of the hexagon, as well as atoms in the center of the hexagon and in the middle of the unit cell.
Hint: Count the positions of atoms in the hexagonal unit cell, including those on the faces and those entirely within the cell.
Step 3: Determine Contribution of Atoms
- Atoms located at the corners of the hexagon contribute only a fraction of their volume to the unit cell because they are shared with adjacent cells.
- Atoms located at the center of the hexagon and those entirely within the cell contribute 100% of their volume to the unit cell.
Hint: Remember that corner atoms contribute 1/6 of their volume to the unit cell, while face-centered and interior atoms contribute fully.
Step 4: Count the Atoms Contributing 100% Volume
In the hexagonal close-packed structure:
- There are 3 atoms located entirely within the unit cell that contribute their full volume.
- The corner atoms do not contribute fully, so they are not included in this count.
Hint: Focus on the atoms that are not shared with other unit cells.
Step 5: Conclusion
Thus, the total number of atoms that contribute their 100% volume within the hexagonal unit cell is 3.
Final Answer: 3 atoms.
---
The hexagonal unit cell is characterized by its unique arrangement of atoms. It is often referred to as the hexagonal close-packed (HCP) structure. In this structure, atoms are arranged in a way that maximizes packing efficiency.
In a hexagonal unit cell, there are typically atoms located at the corners of the hexagon, as well as atoms in the center of the hexagon and in the middle of the unit cell.
- Atoms located at the corners of the hexagon contribute only a fraction of their volume to the unit cell because they are shared with adjacent cells.
- Atoms located at the center of the hexagon and those entirely within the cell contribute 100% of their volume to the unit cell.
In the hexagonal close-packed structure:
- There are 3 atoms located entirely within the unit cell that contribute their full volume.
- The corner atoms do not contribute fully, so they are not included in this count.
Thus, the total number of atoms that contribute their 100% volume within the hexagonal unit cell is 3.
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 18BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 18EXERCISE - CHEMISTRY - SECTION 2
5 Videos
- JEE MAIN REVISION TEST - 13BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 13EXERCISE - CHEMISTRY (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 19BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 19EXERCISE - CHEMISTRY
26 Videos
Similar Questions
Number of atoms in fcc unit cell is
View SolutionIn a simple or primitive unit cell, what is the number of atoms per unit cell ?
View SolutionThe number of atoms per unit cell in bcc lattice is
View SolutionCalculate the number of atoms in a face centred cubic unit cell.
View SolutionThe unit cell present in ABAB, closest packing of atoms is:
View SolutionThe number of atoms per unit cell of the two dimensional square unit cell shown below is:
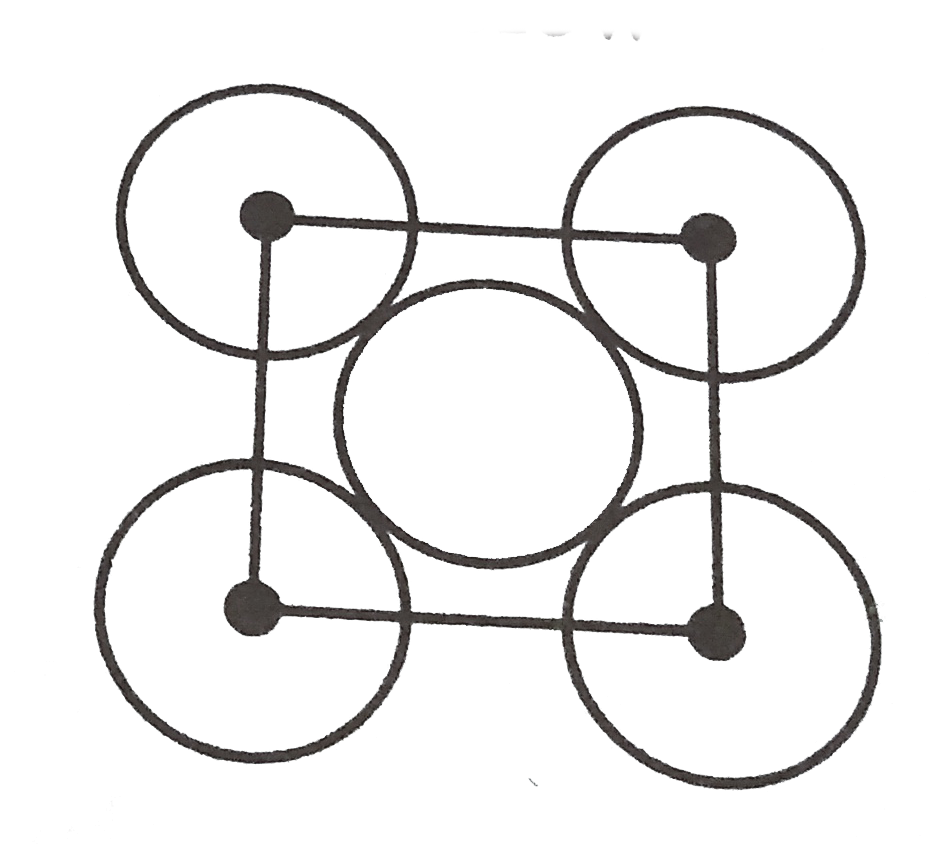
View SolutionHow is simple cubic unit cell formed ? Calculate the number of atoms in a simple unit cell.
View SolutionHow many number of atoms are completely inside the HCP unit cell ?
View SolutionThe unit cell present in ABCABC, closet packing of atoms is:
View SolutionIn hexagonal primitive unit cell, the Corner is shared by:
View Solution
