The self inductance of the motor of an electric fan is 10 H. In order to impart maximum power at 50 Hz, it should be connected to a capacitance of:
(a)1μF
(b)2μF
(c)4μF
(d)8μF
The correct Answer is:A
To solve the problem of determining the capacitance required for maximum power transfer to the motor of an electric fan with a self-inductance of 10 H at a frequency of 50 Hz, we can follow these steps:
1. Understand the Resonance Condition:
For maximum power transfer in an RLC circuit, the inductive reactance (X_L) must equal the capacitive reactance (X_C). This is expressed as:
XL=XC
2. Express Reactances:
The inductive reactance (X_L) is given by:
XL=ωL
where ω is the angular frequency and L is the inductance. The capacitive reactance (X_C) is given by:
XC=1ωC
where C is the capacitance.
3. Relate Inductive and Capacitive Reactance:
Setting XL equal to XC:
ωL=1ωC
4. Solve for Capacitance (C):
Rearranging the equation gives:
ω2C=1L
Thus,
C=1ω2L
5. Calculate Angular Frequency (ω):
The angular frequency ω is related to the frequency f by:
ω=2πf
For f=50 Hz:
ω=2π×50=100πrad/s
6. Substitute Values:
Now substituting ω and L into the capacitance formula:
C=1(100π)2×10
C=110000π2
7. Calculate the Numerical Value:
Using π≈3.14:
C≈110000×(3.14)2≈110000×9.86≈198600≈1.014×10−5F
Converting to microfarads:
C≈10.14μF
8. Final Answer:
The capacitance required to impart maximum power at 50 Hz is approximately 10.14 µF.
For maximum power transfer in an RLC circuit, the inductive reactance (X_L) must equal the capacitive reactance (X_C). This is expressed as:
XL=XC
The inductive reactance (X_L) is given by:
XL=ωL
where ω is the angular frequency and L is the inductance. The capacitive reactance (X_C) is given by:
XC=1ωC
where C is the capacitance.
Setting XL equal to XC:
ωL=1ωC
Rearranging the equation gives:
ω2C=1L
Thus,
C=1ω2L
The angular frequency ω is related to the frequency f by:
ω=2πf
For f=50 Hz:
ω=2π×50=100πrad/s
Now substituting ω and L into the capacitance formula:
C=1(100π)2×10
C=110000π2
Using π≈3.14:
C≈110000×(3.14)2≈110000×9.86≈198600≈1.014×10−5F
Converting to microfarads:
C≈10.14μF
The capacitance required to impart maximum power at 50 Hz is approximately 10.14 µF.
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 18Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 18Exercise:PHYSICS - SECTION 2
Explore 5 Videos
- JEE MAIN REVISION TEST - 13Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 13Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 19Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 19Exercise:PHYSICS
Explore 25 Videos
Similar Questions
The self inductance of a choke coil is 10mH. When it is connected witrh a 10V dc source loss of power is 20watt. When it is connected witrh a 10V ac source loss of power is 10 watt.The frequency of ac source will be:
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 .
.
View Solution(a) What is the reactance of a 2.00H inductor at a frequency of 50.0Hz?
(b) What is the inductance of an inductor whose reactance is 2.00Ω at 50.0Hz?
(c) What is the reactance of a 2.00μF capacitor at a frequency of 50.0Hz?
(d) What is the capacitance of a capacitor whose reactance is 2.00Ω at 50.0Hz?
View SolutionAn AC circuit consists of a resistance and a choke coil in series . The resistance is of 220 Ω and choke coils is of 0.7 H . The power abosorbed from 220 V and 50 Hz , source connected with the circuit , is
View SolutionAn AC circuit consists of a resistance and a choke coil in series . The resistance is of 220 Ω and choke coils is of 0.7 H . The power abosorbed from 220 V and 50 Hz , source connected with the circuit , is
View SolutionThe coefficient of induction of a choke coil is 0.1H and resistance is 12Ω. If it is connected to an alternating current source of frequency 60Hz, then power factor will be
View SolutionThe self-inductance of a choke coil is 10mH. When it is connected with a 10VDC source, then the loss of power is 20watt. When it is connected with 10voltAC source loss of power is 10watt. The frequency of AC source will be
View SolutionA battery of internal resistance 4Ω is connected to the network of the resistance as shown in figure . If the maximum power can be delivered to the network, the magnitude of resistance in Ωshould be
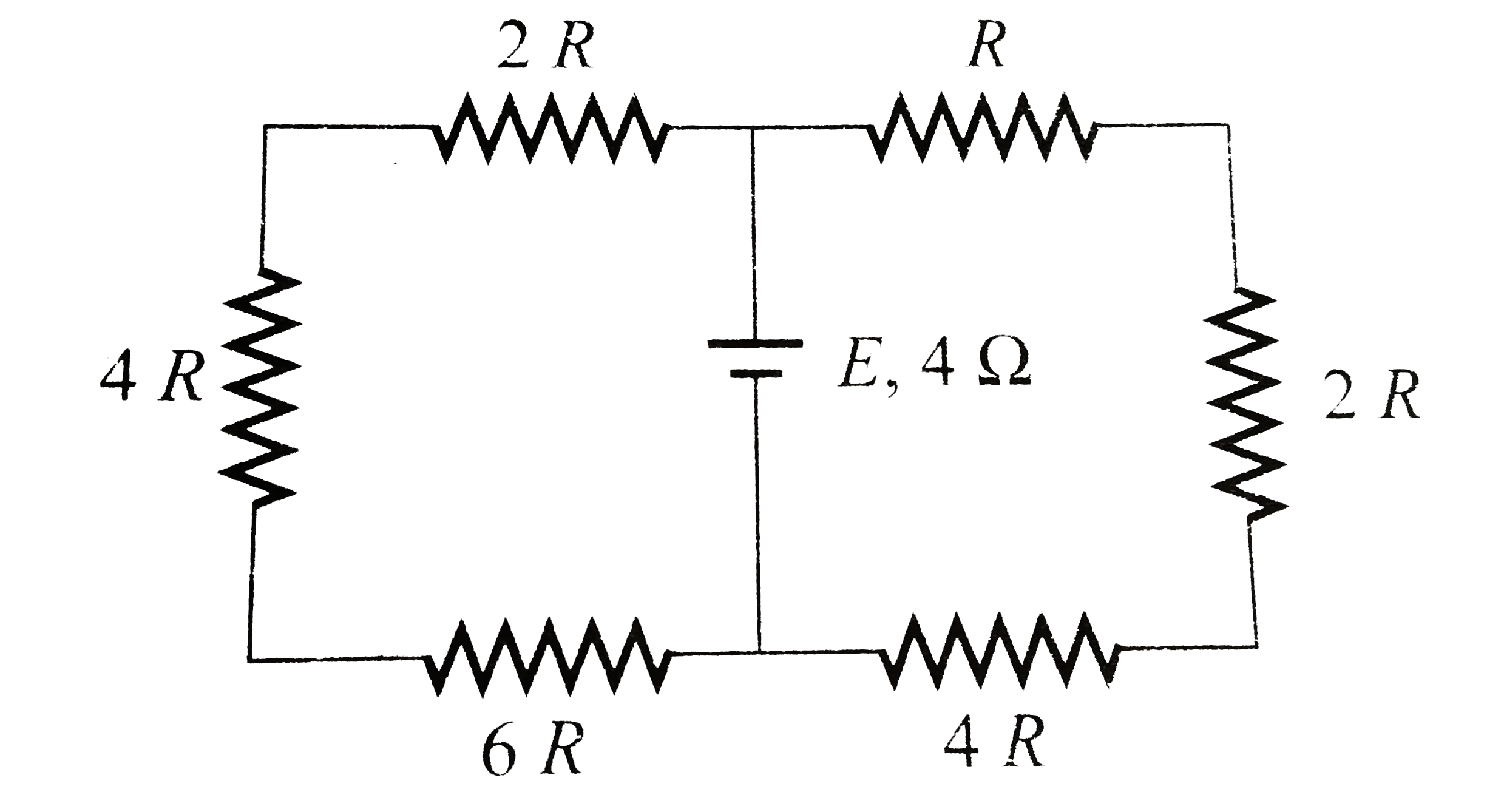
View SolutionA coil having self-inductance of 0.7 H and resistance of 165Ω is connected to an a.c. source of 275 V, 50 Hz. If π=227 Calculate :
Reactance of the coil
View SolutionA circuit has a self inductance of 1H and carries a current of 2A. To prevent sparking when the circuit is switched off, a capacitor which can withstand 400V is used. The least capacitance of the capacitor connected across the switch must be equal to
View Solution

