A loop ABCA of straight edges has three corner points A (8, 0, 0), B (0, 8, 0 ) and C (0, 0, 8). The magnetic field in this region is →B=5(ˆi+ˆj+ˆk)T0 . The quantity of flux through the loop ABCA (in Wb) is _____.
The correct Answer is:D
To find the magnetic flux through the loop ABCA, we will follow these steps:
Step 1: Identify the coordinates of the points A, B, and C
The coordinates are given as:
- A (8, 0, 0)
- B (0, 8, 0)
- C (0, 0, 8)
Step 2: Determine the area of triangle ABC
The triangle ABC is formed by points A, B, and C. We can calculate the area of triangle ABC using the formula for the area of a triangle given by vertices in 3D space:
Area=12∣∣→AB×→AC∣∣
Where:
- →AB=B−A=(0−8,8−0,0−0)=(−8,8,0)
- →AC=C−A=(0−8,0−0,8−0)=(−8,0,8)
Now, we compute the cross product →AB×→AC:
→AB×→AC=∣∣
∣
∣∣^i^j^k−880−808∣∣
∣
∣∣
Calculating the determinant:
=^i(8⋅8−0⋅0)−^j(−8⋅8−0⋅−8)+^k(−8⋅0−8⋅−8)
=^i(64)−^j(−64)+^k(64)
=64^i+64^j+64^k
Now, find the magnitude of the cross product:
∣∣→AB×→AC∣∣=√(64)2+(64)2+(64)2=√3⋅(64)2=64√3
Thus, the area of triangle ABC is:
Area=12⋅64√3=32√3
Step 3: Determine the direction of the area vector
The area vector →A is perpendicular to the plane of the triangle ABC. Since the triangle is in the first octant and the coordinates of A, B, and C are positive, we can take the direction of the area vector as:
→A=32√3^n
Where ^n is the unit vector in the direction of the normal to the triangle. Since →AB and →AC are both in the positive octant, we can take:
^n=1√3(^i+^j+^k)
Thus,
→A=32√3⋅1√3(^i+^j+^k)=32(^i+^j+^k)
Step 4: Calculate the magnetic flux
The magnetic flux Φ through the loop is given by:
Φ=→B⋅→A
Where →B=5(^i+^j+^k) and →A=32(^i+^j+^k).
Calculating the dot product:
Φ=5(^i+^j+^k)⋅32(^i+^j+^k)=5⋅32⋅(1+1+1)=160⋅3=480
Final Answer
Thus, the magnetic flux through the loop ABCA is:
Φ=480Wb
The coordinates are given as:
- A (8, 0, 0)
- B (0, 8, 0)
- C (0, 0, 8)
The triangle ABC is formed by points A, B, and C. We can calculate the area of triangle ABC using the formula for the area of a triangle given by vertices in 3D space:
- →AB=B−A=(0−8,8−0,0−0)=(−8,8,0)
- →AC=C−A=(0−8,0−0,8−0)=(−8,0,8)
∣
∣∣^i^j^k−880−808∣∣
∣
∣∣
=^i(64)−^j(−64)+^k(64)
=64^i+64^j+64^k
The area vector →A is perpendicular to the plane of the triangle ABC. Since the triangle is in the first octant and the coordinates of A, B, and C are positive, we can take the direction of the area vector as:
The magnetic flux Φ through the loop is given by:
Thus, the magnetic flux through the loop ABCA is:
Topper's Solved these Questions
Similar Questions
A loop A(0,0,0)B(5,0,0)C(5,5,0)D(0,5,0)E(0,5,10) and F(0,0,10) of straight edges has six corner points and two sides. The magnetic field in this region is →B=(3ˆi+4ˆk) T. The quantity of flux through the loop ABCDEFA (in Wb) is
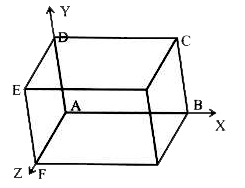
View SolutionA loop A(0,0,0)B(5,0,0)C(5,5,0)D(0,5,0)E(0,5,10) and F(0,0,10) of straight edges has six corner points and two sides. The magnetic field in this region is →B=(3ˆi+4ˆk) T. The quantity of flux through the loop ABCDEFA (in Wb) is

View Solution
Knowledge Check
A square of side x m lies in the x-y plane in a region, when the magntic field is given by →B=B0(3ˆi+4ˆj+5ˆk) T, where B0 is constant. The magnitude of flux passing through the square is
A5B0x2WbB3B0x3WbC2B0x2WbDB0x2Wb
The coordinates of the point equidistant from the points A(0, 0, 0), B(4, 0, 0), C(0, 6, 0) and D(0, 0, 8) is
View SolutionA loop made of straight edges has six corners at A(0,0,0),B(L,O,0),C(L,L,0),D(0,L,0),E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
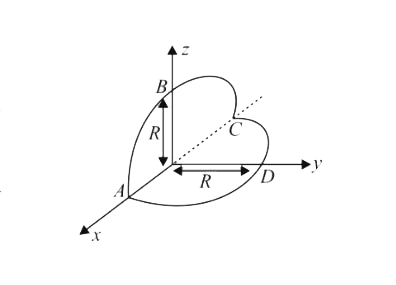
View SolutionA loop has two semi-circular arcs of radii R(=5√πm) each in two mutually perpendicular planes xz & xy as shown in figure. A uniform & constant magnetic field →B=(3ˆi−4ˆj+5ˆk)T exists in the region of the loop. Radius R=5√πm. The quantity of magnetic flux through the loop ABCDA (in Wb) is ............
View Solution
