Pressure difference between two cross sections of a venturimeter, of area & is 480 Pascals.Find the rate of flow of water in the ventrurimeter. ( Density of water )
To solve the problem of finding the rate of flow of water in the venturimeter, we will follow these steps:
Step 1: Identify Given Values
- Area of the wider section (A2) = 40 cm² = 40 × 10⁻⁴ m² = 0.004 m²
- Area of the narrower section (A1) = 20 cm² = 20 × 10⁻⁴ m² = 0.002 m²
- Pressure difference (ΔP) = 480 Pa
- Density of water (ρ) = 1000 kg/m³
Step 2: Apply the Equation of Continuity
The equation of continuity states that:
A1V1=A2V2
Where:
- V1 = velocity at the narrower section
- V2 = velocity at the wider section
From the equation:
V1=A2A1V2
Substituting the areas:
V1=0.0040.002V2=2V2
Step 3: Apply Bernoulli's Equation
According to Bernoulli's equation, the pressure difference can be expressed as:
ΔP=12ρ(V21−V22)
Substituting the expression for V1:
ΔP=12ρ((2V2)2−V22)
ΔP=12ρ(4V22−V22)
ΔP=12ρ(3V22)
ΔP=32ρV22
Step 4: Solve for V2
Rearranging the equation to solve for V2:
V22=2ΔP3ρ
Substituting the known values:
V22=2×4803×1000
V22=9603000=0.32
V2=√0.32≈0.566m/s
Step 5: Find V1
Using the relationship from the continuity equation:
V1=2V2=2×0.566≈1.132m/s
Step 6: Calculate the Rate of Flow (Q)
The volumetric flow rate Q is given by:
Q=A1V1
Substituting the values:
Q=0.002×1.132
Q=0.002264m3/s
To convert to cm³/s:
Q=0.002264×106=2264cm3/s
Final Answer
The rate of flow of water in the venturimeter is approximately 2264 cm³/s.
---
- Area of the wider section (A2) = 40 cm² = 40 × 10⁻⁴ m² = 0.004 m²
- Area of the narrower section (A1) = 20 cm² = 20 × 10⁻⁴ m² = 0.002 m²
- Pressure difference (ΔP) = 480 Pa
- Density of water (ρ) = 1000 kg/m³
The equation of continuity states that:
A1V1=A2V2
Where:
- V1 = velocity at the narrower section
- V2 = velocity at the wider section
V1=A2A1V2
Substituting the areas:
V1=0.0040.002V2=2V2
According to Bernoulli's equation, the pressure difference can be expressed as:
ΔP=12ρ(V21−V22)
ΔP=12ρ((2V2)2−V22)
ΔP=12ρ(4V22−V22)
ΔP=12ρ(3V22)
ΔP=32ρV22
Rearranging the equation to solve for V2:
V22=2ΔP3ρ
Substituting the known values:
V22=2×4803×1000
V22=9603000=0.32
V2=√0.32≈0.566m/s
Using the relationship from the continuity equation:
V1=2V2=2×0.566≈1.132m/s
The volumetric flow rate Q is given by:
Q=A1V1
Substituting the values:
Q=0.002×1.132
Q=0.002264m3/s
To convert to cm³/s:
Q=0.002264×106=2264cm3/s
The rate of flow of water in the venturimeter is approximately 2264 cm³/s.
Topper's Solved these Questions
Similar Questions
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionWater flows in a horizontal tube (see figure). The pressure of water changes by 700 Nm−2 between A and B where the area of cross section are 40cm2 and 20cm2, respectively. Find the rate of flow of water through the tube.

View Solution
Knowledge Check
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103N
Water flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 and 2cm2 respectively. Find the rate of flow of water across any section.
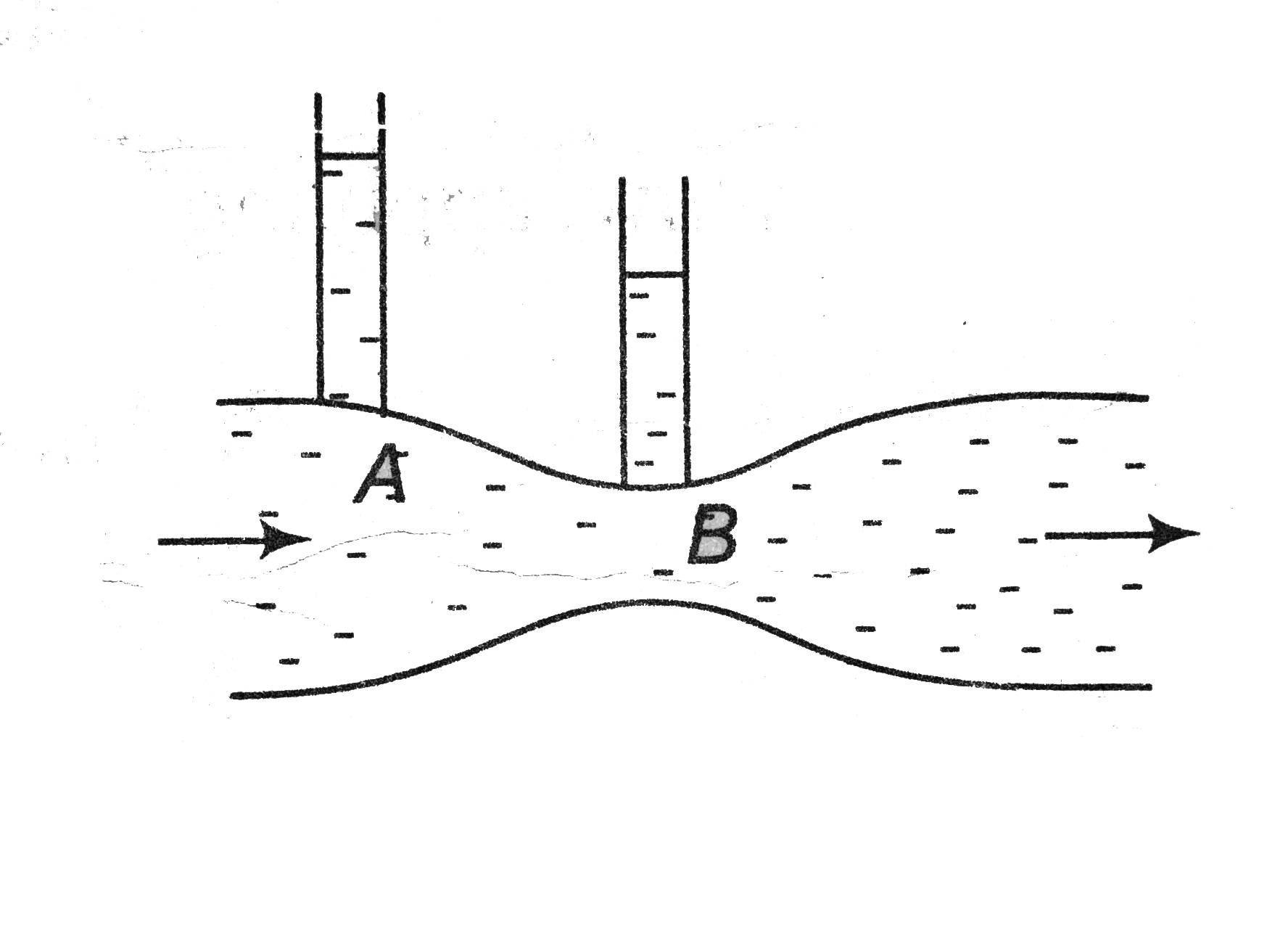 .
.
View SolutionTwo water pipes of diameters 2 cm and 4 cm are connected with the main supply line. The velocity of flow of water in the pipe of 2 cm
View SolutionA 700 g solid cube having an edge of length 10 cm floats in water. How much volume of the cube is outside the water? Density of water =1000kgm−3
View SolutionFlow rate of blood through a capillary of cross - sectional are of 0.25m2 is 100cm3/s. The velocity of flow of blood iis
View SolutionThe area of cross-section of the wider tube shown in fig., is 800cm2 . If a mass of 12 kg is placed on the massless piston, what is the difference in the level of water in two tubes.

View Solution

