Evaluate ∫nπ−π/4−π/4|sinx+cosx|dx,nεN
A
0
B
2n
C
2√2n
D
none of these
Video Solution
Text Solution
The correct Answer is:C
∫nπ−π4−π/4|sinx+cosx|=√2∫nπ−π4−π/4∣∣∣sin(x+π4)∣∣∣dx
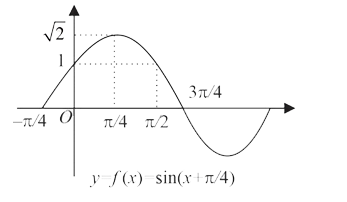
x+π4=t⇒dx=dt
=√2∫nπ0|sint|dx=n√2∫π0sintdt
=n√2(−cos)π0=n√2(1−(−1))
=2√2n
|
Topper's Solved these Questions
Similar Questions
Evaluate: ∫π/4−π/4log(sinx+cosx)dx
View SolutionEvaluate :∫π/4−π/4|sinx|dx
View SolutionEvaluate: ∫π/2−π/2|sinx|dx
View SolutionEvaluate: ∫π/2−π/2log(sinx+cosx)dx
View SolutionEvaluate ∫π4−π4sin2xdx
View SolutionEvaluate ∫π/20|sinx−cosx|dx.
View SolutionEvaluate ∫nπ+t0(|cosx|+|sinx|)dx, where nεN and tε[0,π/2].
View SolutionEvaluate ∫π/40dx1+sinx
View SolutionThe value of ∫π−πsinxf(cosx)dx is
View SolutionEvaluate ∫π2π3ex(1+sinx1+cosx)dx
View Solution
