A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arce of length 3,4 and 5 unit, then the area of the triangle is equal to

A

$\frac{9 \sqrt{3} (\sqrt{1} + \sqrt{3})}{π^{2}}$ sq unit

B

$\frac{9 \sqrt{3} (\sqrt{3} - 1)}{π^{2}}$ sq unit

C

$\frac{9 \sqrt{3} (\sqrt{3} + 1)}{2 π^{2}}$

D

$\frac{9 \sqrt{3} (\sqrt{3} - 1)}{2 π^{2}}$ sq unit

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

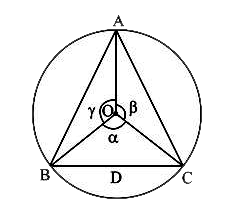
Let arc(BC)=3 , arc(CA)=4 , arc(AB)=5
Let r be the radius of the circle , then
$3 = r α, 4 = r β, 5 = r γ (∵ Angle = \frac{arc}{radius})$
Now , 3+4+5=r $(α + β + γ) = r .2 π \Rightarrow r = \frac{6}{π}$
$△ A B C = △ O B C + △ O C A + △ O A B$
$= \frac{1}{2} r^{2} sin α + \frac{1}{2} r^{2} sin β + \frac{1}{2} r^{2} sin γ = \frac{1}{2} r^{2} {sin (\frac{3}{r}) + sin (\frac{4}{r}) + sin (\frac{5}{r})}$
$= \frac{1}{2} \times \frac{36}{π^{2}} [sin \frac{π}{2} + sin \frac{2 π}{3} + sin \frac{5 π}{6}] = \frac{18}{π^{2}} {1 + \frac{\sqrt{3}}{2} + \frac{1}{2}} = \frac{9 \sqrt{3} (1 + \sqrt{3})}{π^{2}}$ sq unit

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE Main Revision Test-20 | JEE-2020 -MATHEMATICS

Home
Ask Doubt
Profile