The sum of all values of θ∈(0,π2) satisfying sin22θ+cos42θ=34 is :
π
3π2
5π2
None of these
The correct Answer is:B
cos42θ=cos22θ)=0
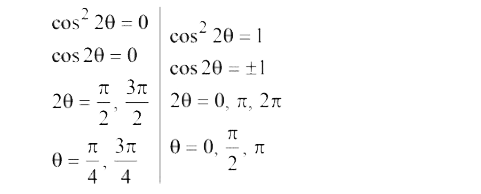
θ∈(0,π)
θ=π4,π2,3π4 ∴ Sum=π4+π2+3π4=6π4=3π2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of values of θ in [0,2π] that satisfies the equation sin2θ−cosθ=14
A4B3C2DNone of these
The number of values of θ in the range [0,2π] satisfying the equation cos42θ+2sin22θ=17(sinθ+cosθ)8 is
View SolutionThe value of θ lying between 0 and π2 and satisfying ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0
View SolutionThe number of values of x lying in [−π,π] and satisfying 2sin2θ=cos2θandsin2θ+2cos2θ−cosθ−1=0 is
View SolutionThe possible value of θ∈[−π,π] satisfying the equation 2(cosθ+cos2θ)+(1+2cosθ)sin2θ=2sinθ are
View SolutionIf θ1 and θ2 be respectively the smallest and the largest values of θ in (0,2π)−(π) which satisfy the equation, 2cot2θ−5sinθ+4=0, then ∫θ2θ1cos23θdθ is equal to :
View SolutionThe value of theta lying between 0 and π2 and satisfying the equation ∣∣(1+cos2θ,sin2θ,4sin4θ),(cos2θ,1+sin2θ,4sin4θ)(cos2θ,sin2θ,1+4sin4θ)∣∣=0 is (are)
View SolutionThe number of values of θ∈[−3π2,4π3] which satisfies the system of equations.
2sin2θ+sin22θ=2and
sin2θ+cos2θ=tanθ is
View Solution

