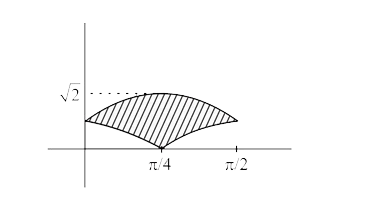
The area enclosed by the curve y=sinx+cosxandy=|cosx−sinx| over the interval [0,π2] is (a)4(√2−2) (b) 2√2 (√2 -1) (c)2(√2 +1) (d) 2√2(√2+1)
4(√2−1)
2√2(√2−1)
2(√2+1)
2√2(√2+1)
The correct Answer is:B
Required area =π/4∫0|2sinx|dx+π/2∫π/4|2cosx|dx=2√2(2√2−1)
Topper's Solved these Questions
Similar Questions
The area enclosed by the curves y=sinx+cosxandy=|cosx−sinx| over the interval [0,π2] is (a) 4(√2−1) (b) 2√2(√2−1) (c) 2(√2+1) (d) 2√2(√2+1)
View SolutionThe value of √3−2 √2 is
(a)√2−1
(b) √2+1
(c) √3−√2
(d) √3+ √2
View Solution∫√20[x2]dx is equal to (A) 2−√2 (B) 2+√2 (C) √2−1 (D) √2−2
View SolutionThe area under the curve y=|cosx−sinx|,0≤x≤π2, and above x-axis is: (A) 2√2+2 (B) 0 (C) 2√2−2 (D) 2√2
View SolutionThe value of the definite integral ∫π20√tanxdx is √2π (b) π√2 2√2π (d) π2√2
View Solution1√9− √8 is equal to:
(a)3+2√2
(b) 13+2√2
(c) 3−2√2
(d) 32− √2
View SolutionIf (0,1),(1,1)and(1,0) be the middle points of the sides of a triangle, its incentre is (2+√2,2+√2 ) (b) [2+√2,−(2+√2)] (2−√2,2−√2) (d) [2−√2,(2+√2)]
View SolutionIf (0,1),(1,1)and(1,0) be the middle points of the sides of a triangle, its incentre is (2+√2,2+√2 ) (b) [2+√2,−(2+√2)] (2−√2,2−√2) (d) [2−√2,(2+√2)]
View SolutionThe value of x in (0,π2) satisfying √3−1sinx+√3+1cosx=4√2 is / are
View Solution(√8)13=?
(a) 2
(b) 4
(c) √2
(d) 2√2
View Solution

