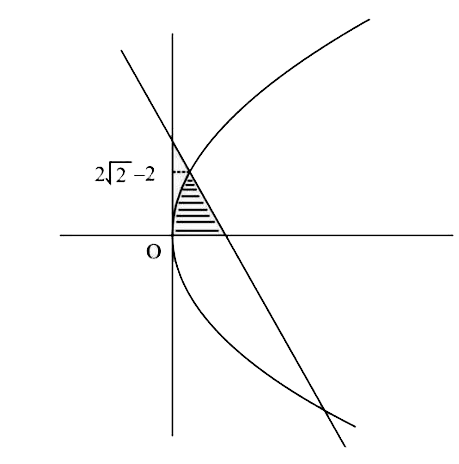
If the area (in sq. units) of the region
${(x, y) : y^{2} \leq 4 x, x + y \leq 1, x \geq 0, y \geq 0}$ is $a \sqrt{2} + b$ , then $a - b$ is equal to :

A

$\frac{8}{3}$

B

$\frac{10}{3}$

C

$- \frac{2}{3}$

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$A = \int_{0}^{2 \sqrt{2} - 2} (1 - y \frac{y^{2}}{4}) d y$
$A = {[y - \frac{y^{2}}{2} - \frac{y^{3}}{12}]}_{0}^{2 \sqrt{2} - 2} = y [1 - \frac{y}{2} - \frac{y^{2}}{12}]$
$= 2 (\sqrt{2} - 1) [1 - (\sqrt{2} - 1) - \frac{4}{12} {(\sqrt{2} - 1)}^{2}]$
$= 2 (\sqrt{2} - 1) [2 - \sqrt{2} - \frac{1}{3} (2 + 1 - 2 \sqrt{2})]$
$= 2 (\sqrt{2} - 1) [1 - \frac{\sqrt{2}}{3}] = 2 (\sqrt{2} - \frac{2}{3} = 1 + \frac{\sqrt{3}}{3})$
$= 2 (\frac{4}{3} \sqrt{2} - \frac{5}{3})$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST- 16-MATHEMATICS (SECTION 2)

Home
Ask Doubt
Profile