A thin ring of 10 cm radius carries a uniformly distributed charge. The ring rotates at a constant. speed of 1200 r.p.m. about its axis passing through the centre of the ring perpendicular to ity plane. Find the charge carried by the ring, if the magnetic field induction in its centre is 3.8XX10−9T.
3×10−5C
7×10−6C
4×10−5C
2×10−6C
The correct Answer is:A
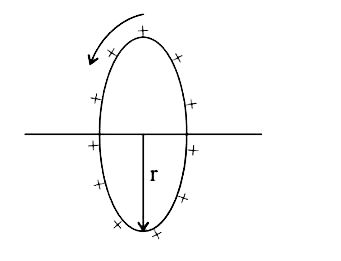
ω=2πT B=μ04πIrϕ
I=qT B=μ04πIr.2π
I=q2π/ω B=μ04π.2πIr
I=qω2π 3.8×10−9=10−7×2π×qω2πr
3.8×10−9=10−7×q×40π10×10−2
q=3.8×10−9×10×10−240π×10−7
q=3.8×10−10×10740×227
q=3.8×10−3×740×22
q=0.030×10−3C
q=3×10−5C
Topper's Solved these Questions
- JEE MAIN REVISION TEST- 16Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST- 16Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST 8 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST 8 (2020)Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST- 24 Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST- 24 Exercise:PHYSICS ( SECTION - 2)
Explore 5 Videos
Similar Questions
A charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?

View Solution