A bacterial infection in an internal wound grows as N'(t)=N0exp(t), where the time t is in hours.A dose of antibiotic, taken orally, needs 1 hour to reach the wound. Once it reaches there, the bacterial population goes down as dNdt=−5N2. What will be the plot of N0N vs. t after 1 hour?
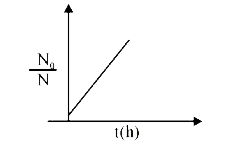
The correct Answer is:B
To solve the problem, we need to analyze the growth of the bacterial population and the effect of the antibiotic over time. Let's break it down step by step.
Step 1: Determine the bacterial population before the antibiotic reaches the wound
The growth of the bacterial population is given by the equation:
N′(t)=N0et
where N0 is the initial population at t=0.
To find the population at t=1 hour, we can integrate this equation:
N(t)=∫N′(t)dt=∫N0etdt=N0et+C
At t=0, N(0)=N0, so:
N(0)=N0e0+C
N0=N0+C
Thus, C=0.
Therefore, the bacterial population at t=1 hour is:
N(1)=N0e1=N0e
Step 2: Analyze the effect of the antibiotic after it reaches the wound
After 1 hour, the antibiotic starts to take effect, and we have the differential equation:
dNdt=−5N2
We can rearrange this equation:
dNN2=−5dt
Step 3: Integrate the equation
Integrating both sides:
∫dNN2=∫−5dt
This gives:
−1N=−5t+C′
Step 4: Determine the constant of integration
At t=1, we know N(1)=N0e:
−1N0e=−5(1)+C′
C′=1N0e+5
Step 5: Substitute back to find N(t)
Now substituting C′ back into the integrated equation:
−1N=−5t+(1N0e+5)
Rearranging gives:
1N=5t−1N0e−5
Step 6: Find N0N
Taking the reciprocal:
N0N=N0e5N0e(5t−5−1N0e)
This simplifies to:
N0N=5N0e(5t−5−1N0e)
Step 7: Plot N0N vs. t
The relationship we derived is linear in terms of t, indicating that the plot of N0N vs. t will be a straight line.
Conclusion
The plot of N0N vs. t after 1 hour will be a straight line with a positive slope.
---
N′(t)=N0et
where N0 is the initial population at t=0.
N(t)=∫N′(t)dt=∫N0etdt=N0et+C
N(0)=N0e0+C
N0=N0+C
Thus, C=0.
N(1)=N0e1=N0e
dNdt=−5N2
dNN2=−5dt
∫dNN2=∫−5dt
This gives:
−1N=−5t+C′
−1N0e=−5(1)+C′
C′=1N0e+5
−1N=−5t+(1N0e+5)
Rearranging gives:
1N=5t−1N0e−5
N0N=N0e5N0e(5t−5−1N0e)
This simplifies to:
N0N=5N0e(5t−5−1N0e)
Topper's Solved these Questions
- JEE MAIN REVISION TEST -14 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -14 EXERCISE - CHEMISTRY (SECTON 2)
5 Videos
- JEE MAIN REVISION TEST - 7|JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Chemistry (Section - 2) Numercial Value type
5 Videos
- JEE MAIN REVISION TEST -17 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -17 (2020)EXERCISE - CHEMISTRY
25 Videos
Similar Questions
Knowledge Check
Miriam and Jessica are growing bacteria in a laboratory. Miriam uses the growth function f(t)=n2t to model her experiment while Jessica uses the function g(t)=(n2)4t to model her experiment. In each case, n represents the initial number of bacteria, and t is the time, in hours. If Miriam starts with 6 bacteria, how many bacteria should Jessica start with to achieve the same growth over time?
A32B16C8D4
Find the decay rate of the substance having 4×1015 atoms. Half life of a radioactive substances in α-decay is 1.2×107 is
View SolutionFor the functions f(x)=∫x0sinttdt where x>0. At x=nπ f(x) attains
View Solutionselect the correct representation of density of population (N) which can be expressed after a period of time t+1.
View SolutionInternal energy of n moles of helium at temperature T1K is equal to the internal energy of 2n moles of oxygen gas at temperature T2K then the value of T1T2will be
View SolutionWrite the indicated terms in each of the following sequences whose nth terms are: tn=n2(n+1):t4,t5
View SolutionIf in Bohr's model, for unielectronic atom, time period of revolution is represented as Tn,z where n represents shell no. and Z represents atomic number then the value of T1,2:T2,1 , will be :
View SolutionIf (7+4√3)n+5+t , where n and s are
positive integers and t is a proper fraction , show that
(1 - t) (s + t) = 1
View Solution
