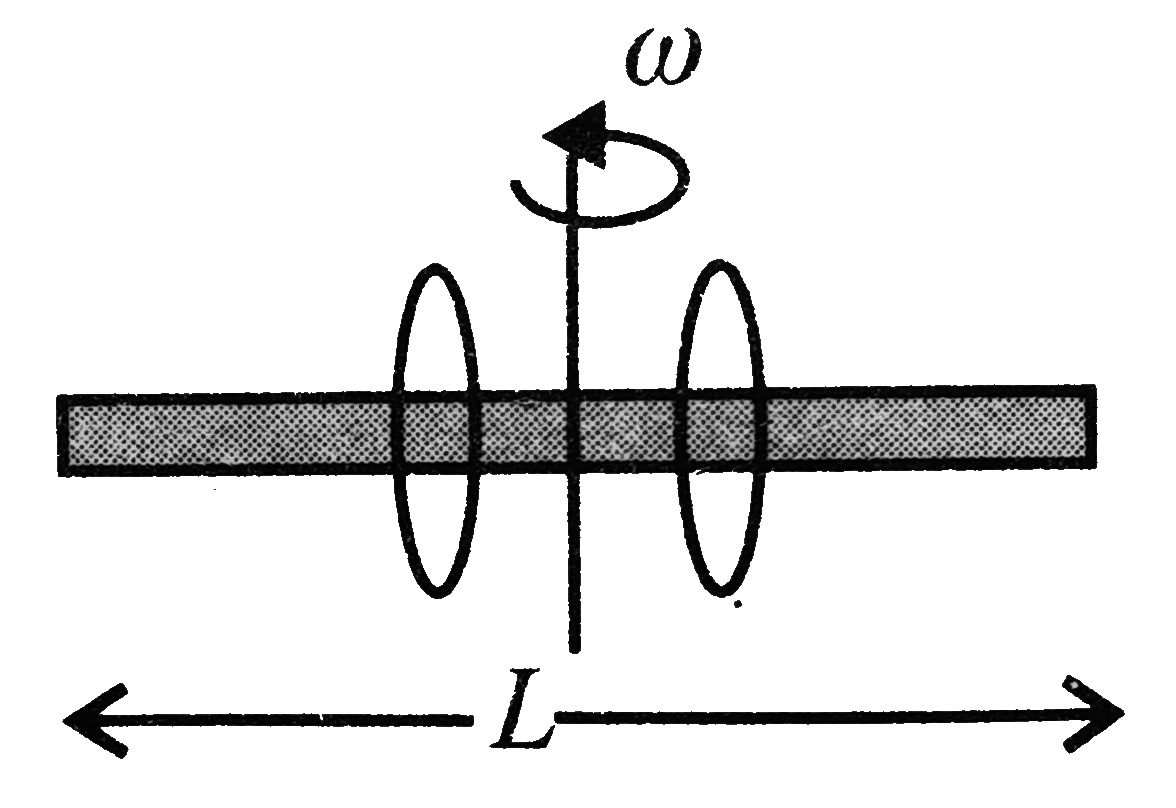
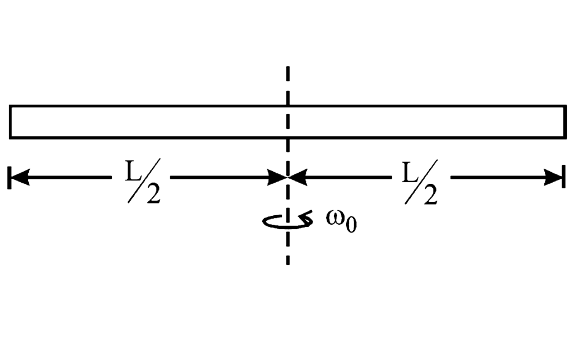
A smooth uniform rod of length L and mass M has two identical beads (1 and 2) of negligible size, each of mass m, which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with angular velocity ω0 about an axis perpendicular to the rod and is passing through its midpoint. There are no external forces when the beads reach the ends of the rod, the angular velocity of the system is
Mω0M+6m
Mω0M+3m
Mω0M+2m
Mω0M+m
The correct Answer is:A
Conservation of angular momentum
[ML212+2m(0)2]ω0[ML212+2×m(L2)2]ω,ω=Mω0M+6m
Topper's Solved these Questions
- JEE MAIN REVISION TEST 11 (2020) BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 11 (2020) EXERCISE - PHYSICS (SECTION - 2)
5 Videos
- JEE MAIN REVISION TEST -17 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -17 (2020)EXERCISE - PHYSICS
25 Videos
- JEE MAIN REVISION TEST 5 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 5 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
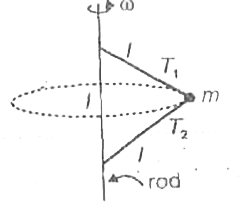
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA thin smooth rod of length L and mass M is rotating freely with angular speed ω0 about an axis perpendicular ot the rod and passing through its centre. Two beads of mass m and negligible sizer are at the center of the rod intially. The beads are free to slide along the rod. the angular speed of the system, when the beads reach the oppsite ends of rod, will be :
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View Solution
