A capacitor of capacitance is charged with voltage . The electric field inside the capacitor with dielectric is and the area of the plate , then the dielectric constant of the medium is : in S.I units) (A) (B) (C) (D)
6.2
4.5
8.5
3.8
The correct Answer is:C
To find the dielectric constant k of the medium in the capacitor, we can follow these steps:
Step 1: Write down the known values
- Capacitance C=15pF=15×10−12F
- Voltage V=500V
- Electric Field E=106V/m
- Area of the plates A=10−4m2
- Permittivity of free space ϵ0=8.85×10−12F/m
Step 2: Use the relationship between electric field, voltage, and distance
The electric field E is related to the voltage V and the distance d between the plates of the capacitor by the formula:
E=Vd
From this, we can express d as:
d=VE
Step 3: Substitute the known values to find d
Substituting the known values:
d=500V106V/m=0.0005m=5×10−4m
Step 4: Use the capacitance formula
The capacitance C of a capacitor with a dielectric is given by:
C=ϵAkd
Where:
- ϵ=ϵ0k (the permittivity of the dielectric material)
Step 5: Rearrange the capacitance formula to solve for k
Rearranging the formula for k:
k=Cdϵ0A
Step 6: Substitute the known values into the formula for k
Substituting the values we have:
k=(15×10−12F)(5×10−4m)(8.85×10−12F/m)(10−4m2)
Step 7: Calculate k
Calculating the numerator:
15×10−12×5×10−4=75×10−16F m
Calculating the denominator:
8.85×10−12×10−4=8.85×10−16F
Now, substituting these into the equation for k:
k=75×10−168.85×10−16≈8.47
Conclusion
Thus, the dielectric constant k of the medium is approximately 8.47.
Final Answer
The correct option is (B) 8.47.
- Capacitance C=15pF=15×10−12F
- Voltage V=500V
- Electric Field E=106V/m
- Area of the plates A=10−4m2
- Permittivity of free space ϵ0=8.85×10−12F/m
The electric field E is related to the voltage V and the distance d between the plates of the capacitor by the formula:
E=Vd
From this, we can express d as:
d=VE
Substituting the known values:
d=500V106V/m=0.0005m=5×10−4m
The capacitance C of a capacitor with a dielectric is given by:
C=ϵAkd
Where:
- ϵ=ϵ0k (the permittivity of the dielectric material)
Rearranging the formula for k:
k=Cdϵ0A
Substituting the values we have:
k=(15×10−12F)(5×10−4m)(8.85×10−12F/m)(10−4m2)
Calculating the numerator:
15×10−12×5×10−4=75×10−16F m
Calculating the denominator:
8.85×10−12×10−4=8.85×10−16F
Now, substituting these into the equation for k:
k=75×10−168.85×10−16≈8.47
Thus, the dielectric constant k of the medium is approximately 8.47.
The correct option is (B) 8.47.
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 10| JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 10| JEE -2020EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 1 | JEE - 2020 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 1 | JEE - 2020 EXERCISE - PHYSICS ( SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 12 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 12 EXERCISE - PHYSICS
25 Videos
Similar Questions
Voltage rating of a parallel plate capacitor is 500V. Its dielectric can withstand a maximum electric field of 106V/m. The plate area is 10−4m2. What is the dielectric constant if the capacitance is 15pF?
(given ε0=8.86×10−12C2/Nm2)
View SolutionIf electric field is changing at rate of 6×106 V/ms between the plates of a capacitor. Having plate areas 2.0cm2, then the displacement current is
View SolutionAn isolated capacitor of capacitance C is charged to a potential V. Then a dielectric slab of dielectric constant K is inserted as shown. The net charge on four surfaces 1,2, 3 and 4 would be respectively.

View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionA capacitor of capacitance 10(μ)F is connected to a battery of emf 2V.It is found that it takes 50 ms for the charge on the capacitor to bacome 12.6(μ)C.find the resistance of the circuit.
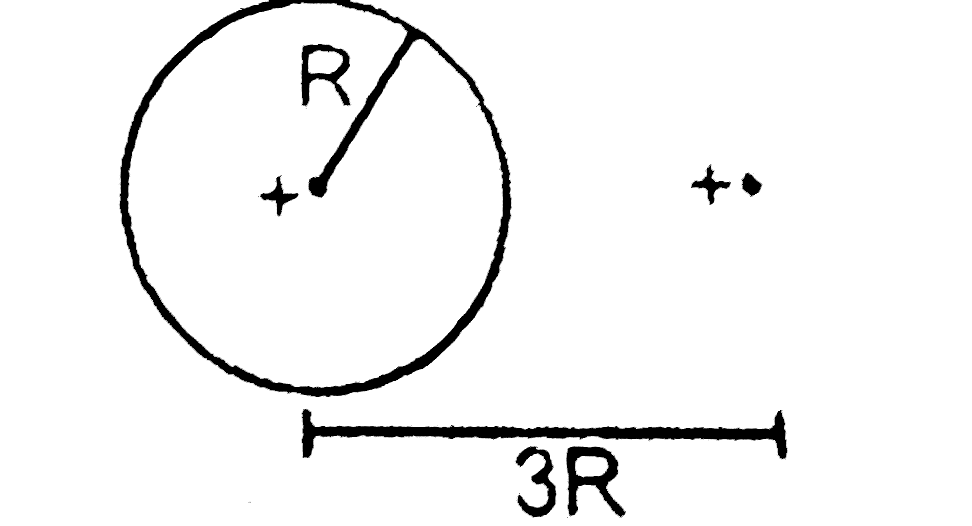
View SolutionFind the flux of the electric field through a spherical surface of radius R due to a charge of 8.85×10−8C at the centre and another equal charge at a point 3R away from the centre (Given : ε0=8.85×10−12 units )
View SolutionThe surface density of charge on the surface of a charged conductor in the air is 26.5μCm−2 . The the outward force per unit area of the charged conductor is (ε0=8.85×10−12C2N−1m−2)
View Solution
