A student scores the following marks in five tests 45, 54, 41, 57, 43. His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
(a) 1003
(b) 103
(c) 10√3
(d) 100√3
To solve the problem step by step, we can follow these instructions:
Step 1: Calculate the total score for the six tests
We know the mean score for the six tests is 48. The formula for mean is given by:
Mean=Sum of all observationsTotal number of observations
Given that the mean is 48 and there are 6 tests, we can write:
48=45+54+41+57+43+x6
where x is the score of the sixth test.
Step 2: Calculate the sum of the scores from the first five tests
Now, let's calculate the sum of the scores from the first five tests:
45+54+41+57+43=240
Step 3: Set up the equation to find x
Now we can substitute this sum back into the equation:
48=240+x6
Step 4: Multiply both sides by 6 to eliminate the fraction
Multiplying both sides by 6 gives:
288=240+x
Step 5: Solve for x
Now, we can solve for x:
x=288−240=48
Step 6: Calculate the standard deviation
Now that we have all six scores: 45, 54, 41, 57, 43, and 48, we can calculate the standard deviation. The formula for standard deviation (σ) is:
σ=√∑(x2i)n−¯x2
where n is the number of observations and ¯x is the mean.
Step 7: Calculate the mean ¯x
The mean is already given as 48.
Step 8: Calculate the sum of squares of the scores
Now, we calculate the sum of the squares of each score:
∑(x2i)=452+542+412+572+432+482
Calculating each square:
- 452=2025
- 542=2916
- 412=1681
- 572=3249
- 432=1849
- 482=2304
Now, summing these:
2025+2916+1681+3249+1849+2304=14024
Step 9: Substitute into the standard deviation formula
Now substituting into the standard deviation formula:
σ2=140246−482
Calculating 482:
482=2304
Now substituting back:
σ2=140246−2304
Calculating 140246:
140246=2337.33
Now, substituting this value:
σ2=2337.33−2304=33.33
Step 10: Calculate the standard deviation
Now, taking the square root to find σ:
σ=√33.33≈5.77
Final Answer
Thus, the standard deviation of the marks in the six tests is approximately 5.77.
---
We know the mean score for the six tests is 48. The formula for mean is given by:
Now, let's calculate the sum of the scores from the first five tests:
Now we can substitute this sum back into the equation:
Multiplying both sides by 6 gives:
Now, we can solve for x:
Now that we have all six scores: 45, 54, 41, 57, 43, and 48, we can calculate the standard deviation. The formula for standard deviation (σ) is:
The mean is already given as 48.
Now, we calculate the sum of the squares of each score:
- 542=2916
- 412=1681
- 572=3249
- 432=1849
- 482=2304
Now substituting into the standard deviation formula:
Now, taking the square root to find σ:
Thus, the standard deviation of the marks in the six tests is approximately 5.77.
Topper's Solved these Questions
- JEE Main Revision Test-9 | JEE-2020 Book:VMC MODULES ENGLISHChapter:JEE Main Revision Test-9 | JEE-2020 Exercise:SECTION 2
Explore 5 Videos
- JEE Main Revision Test-6 | JEE-2020Book:VMC MODULES ENGLISHChapter:JEE Main Revision Test-6 | JEE-2020Exercise:MATHEMATICS
Explore 25 Videos
- JEE MAIN REVISON TEST-23Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISON TEST-23Exercise:MATHEMATICS (SECTION 2)
Explore 5 Videos
Similar Questions
Knowledge Check
A student's mean score on 5 tests was 84. The student's mean score on the first 4 of these tests was 87. What was the student's score on the fifth of these tests ?
A68B72C75D81
The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
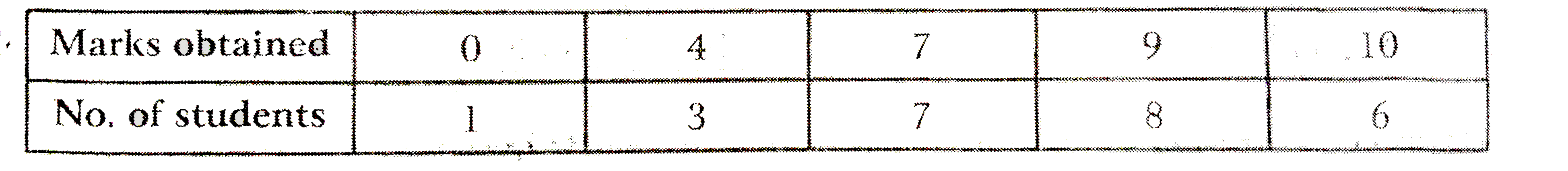
View SolutionIf for somex∈R, the frequency distribution of the marks obtained by 20 students in a test is:

Then the mean of the marks is:
View SolutionCalculate the mean of the scores of 20 students in a mathematics test
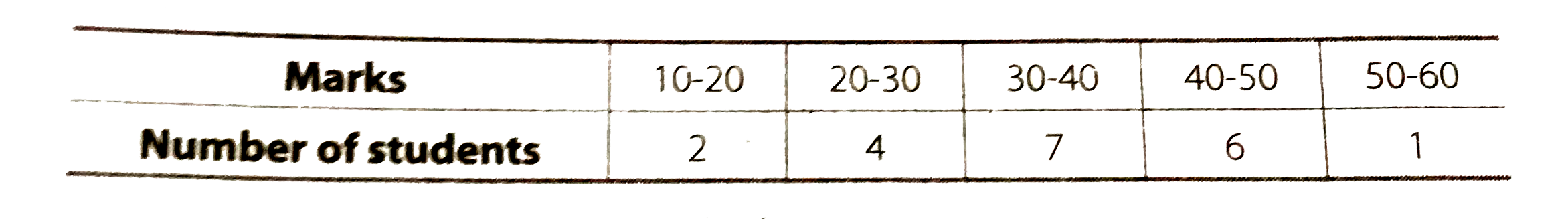
View SolutionFind the mode of the following frequency table, which gives the marks scored by 40 students in a test:
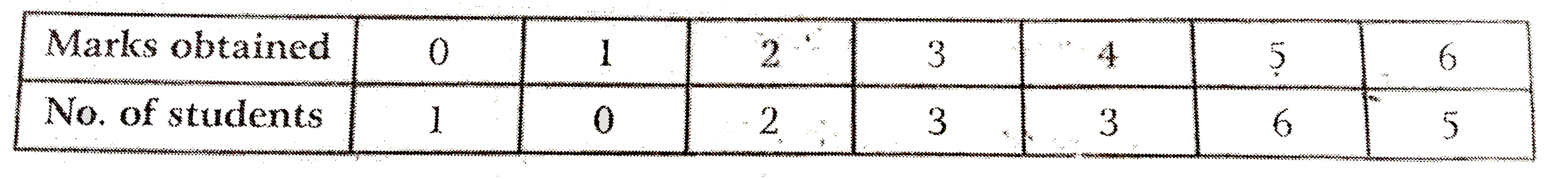
View SolutionOn a test that has normal distribution of scores, a score of 58 falls two standard deviation below the mean, and a score of 85 is one standard deviation above the mean. What is the mean score of this test?
View SolutionOn a test that has a normal distribution of scores of 59 falls two standard deviations below the mean, and score of 74 is one standard deviation above the mean. If x is an integer score that lies between 2.5 and 3.0 standard deviations above the means. What is a possible value of x?
View SolutionA batsman scored the following number of runs in six innings:36, 35, 50, 46, 60, 55Calculate the mean runs scored by him in an inning.
View Solution


