The height of a right circular cylinder of maxium volume inscribed in a sphere of radius 3 cm is

A

A. $\sqrt{6}$

B

B. $\sqrt{3}$

C

C. $\frac{2}{3} \sqrt{3}$

D

D. $2 \sqrt{3}$

Video Solution

Text Solution

Verified by Experts

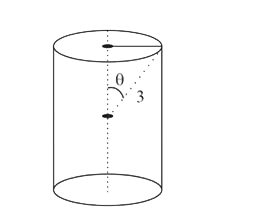
$h = 2 (3 cos θ)$
$r = 3 sin θ, v = π r^{2} h, = π 9 {sin}^{2} θ . 6 cos θ$
$V = 54 π sin 2 θ cos θ, \frac{d v}{d θ} = 0$
$\Rightarrow 2 sin θ {cos}^{2} θ - {sin}^{3} θ = 0 \Rightarrow 2 s (1 - s^{2}) - s^{3} = 0 \Rightarrow 2 s - 2 s^{3} - s^{3} = 0$
$\Rightarrow 2 s - 3 s^{3} = 0 \Rightarrow s = 0 or 2 - 3 s^{2} = 0$
$s = \pm \sqrt{\frac{2}{3}} ∴ cos θ = \sqrt{1 - \frac{2}{3}} = \frac{1}{\sqrt{3}}$
$h = 6 (\frac{1}{\sqrt{3}}), h = 2 \sqrt{3}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a right circular cylinder of height 10 is inscribed in a sphere of radius 6, what is the volume of the cylinder ?
A104
B346
C545
D785

VMC MODULES ENGLISH-JEE Main Revision Test-9 | JEE-2020 -SECTION 2

Home
Ask Doubt
Profile