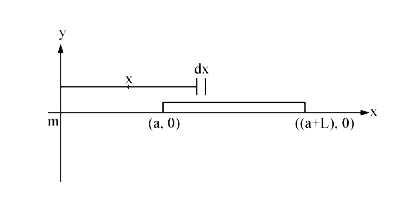
A straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
Gm[A(1a+L−1A)−BL]
Gm[A(1a−1a+L)+BL]
Gm[A(1a+L−1a)+BL]
Gm[A(1a−1a+L)−BL]
The correct Answer is:B
dm=rdx
=(A+Bx2)dx
F=∫a+LaGmdMx2=Gm∫a+La(A+Bx2dx)dxx2
=Gm[∫a+LaAx2dx+a∫a+LaBdx]
F=4m[A(1a−1a+L)]=BL
=GM[A(La(a+L))+Bl]
 .
.
Topper's Solved these Questions
- JEE MAIN REVISION TEST 8 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 8 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST 5 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 5 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST- 16BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 16EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
A straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionA straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionA straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionA straight rod of length 'l' extends from x=l to x=2l. If linear mass density of rod is μ=(μ0l3X3), then the gravitational force exerted by rod on a particle of mass m at x=0 , is
View SolutionFind the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
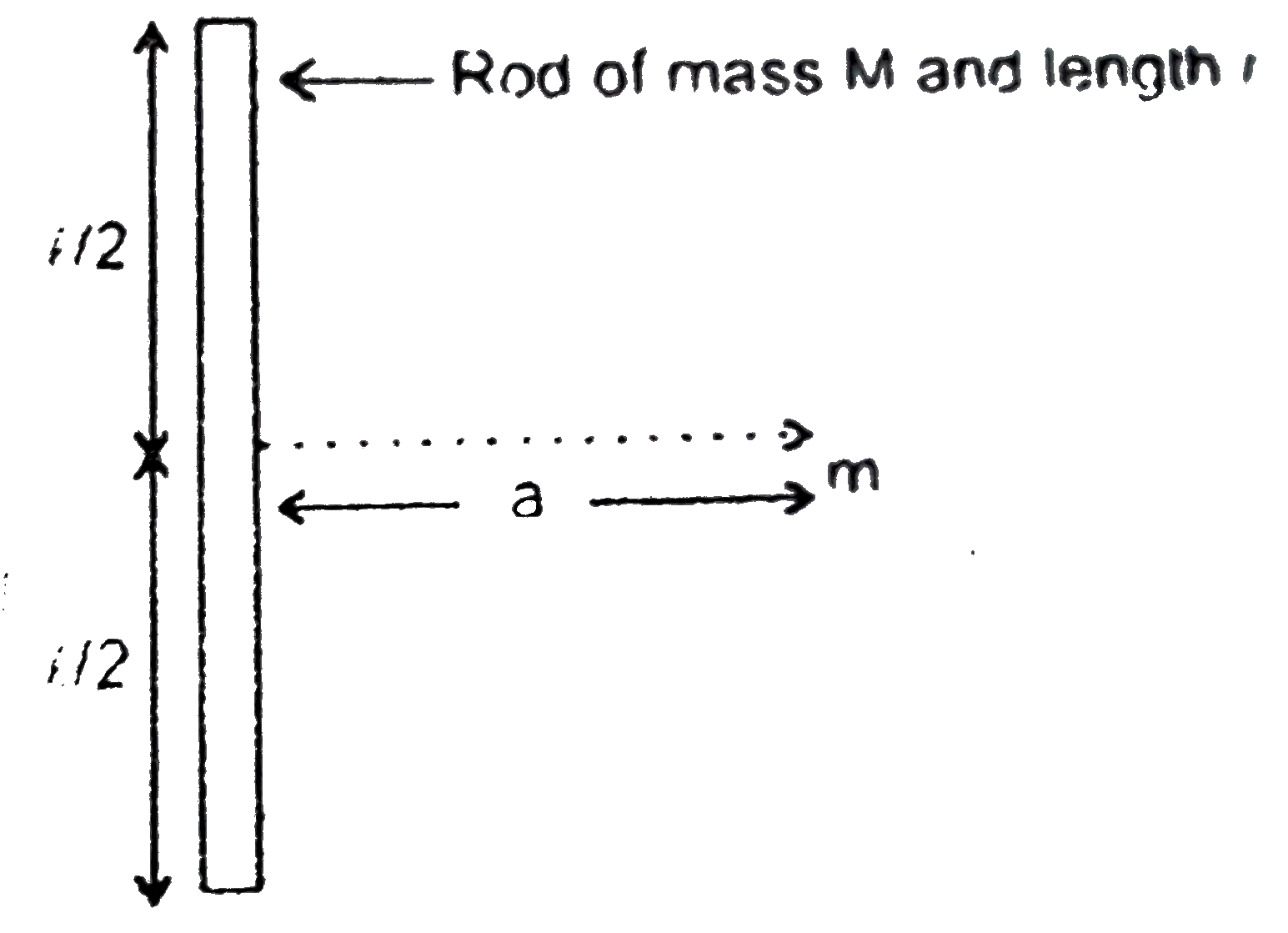
View SolutionCalculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA thin bar of length L has a mass per unit length λ, that increases linerarly with distance from one end. If its total mass is M and its mass per unit length at the lighter end is λ0, then the distance of the centre of mass from the lighter end is
View SolutionA thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.

View Solution
