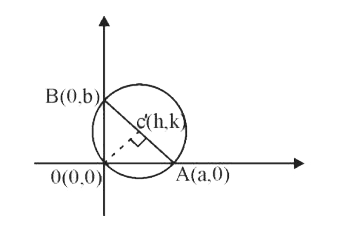
A circle of constant radius r passes through the origin O, and cuts the axes at A and B. The locus of the foots the perpendicular from O to AB is ${(x^{2} + y^{2})}^{k} = 4 r^{2} x^{2} y^{2}$ , Then the value of k is

A

$(x^{2} + y^{2}) (x + y) = R^{2} x y$

B

${(x^{2} + y^{2})}^{3} = 4 R^{2} x^{2} y^{2}$

C

${(x^{2} + y^{2})}^{2} + 4 R x^{2} y^{2}$

D

$(x^{2} + y^{2}) = 4 R^{2} x^{2} y^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

let A be (a, 0) and B be (0, b) as at a right angle is formed so AB wil act as diameter of circle. So,
$\sqrt{a^{2} + b^{2}} = 2 R$
$a^{2} + b^{2} = 4 R^{2}$ …(i)
Let c'(h,k) be required locus.
Also, $∠ O C' A = 90^{\circ}$
So. In $Δ O C' A$
$O A^{2} = {(O C')}^{2} + {(A C')}^{2}$
$a^{2} = h^{2} + k^{2} + {(h - a)}^{2} + {(k - 0)}^{2}$
$a^{2} = h^{2} + k^{2} + h^{2} + a^{2} - 2 a h + k^{2}$
$2 (h^{2} + k^{2} - a h) = 0$
$a = \frac{h^{2} + k^{2}}{h}$ ...(ii)
Similarly $b = \frac{h^{2} + k^{2}}{k}$ ...(iii)
Put (ii) & (iii) in (i)
$[\frac{h^{2} + k^{2}}{h}] + [\frac{h^{2} + k^{2}}{k}] = 4 R^{2} \Rightarrow [h^{2} + k^{2}] = 4 R^{2} [h^{2} k^{2}]$ Put $h \to x, k \to y$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST - 7|JEE - 2020-Mathematics (Section - 2) Numercial type questions

Home
Ask Doubt
Profile