Two circles with equal are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the order circle. Then the distance between the centres of these circles is.
√2
2
1
2√2
The correct Answer is:B
PC1=PC2 =r (say )
⇒ΔC1PC2 is isosceles
⇒ (PM) is perpendicular to (C1C2) and bisects ∠C1PC2
Also PC1 is tangent ⇒PC1 is perpendicular to PC2
⇒∠C1PM=45∘=∠C2PM
⇒PC1=√2=PC2{∵cos45∘=1r}
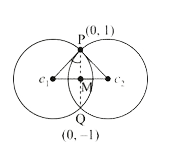
⇒(C1C2)=√2+2=2
Topper's Solved these Questions
Similar Questions
Two circles with equal radii are intersecting at the points (0, 1) and (0,-1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View SolutionIf the line x+3y=0 is tangent at (0,0) to the circle of radius 1, then the centre of one such circle is
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionA circle passes through (0,0) and (1,0) and touches the circle x2+y2=9 then the centre of circle is -
View SolutionThe line x = y touches a circle at the point (1, 1). If the circle also passes through the point (1, -3). Then its radius is 0
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The square of the radius of the circle is
View SolutionIf a circle passes through the points (0,0),(a,0)and(0,b), then find the coordinates of its centre.
View Solution