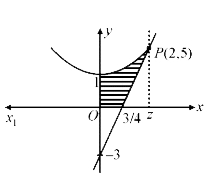
The area (in sq. units) in the first quadrant bounded by the parabola $y = x^{2} + 1$ , the tangent to it at the point (2, 5) and the coordinate axes is

A

$\frac{37}{24}$

B

$\frac{14}{3}$

C

$\frac{8}{3}$

D

$\frac{187}{24}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of tangent to the parabola $y = x^{2} + 1 a t (2, 5) i s 4 x - y - 3 = 0$
Required Area
$= \int_{0}^{2} (x^{2} + 1) d x - \frac{1}{2} \times \frac{5}{4} \times 5$
$= \frac{x^{3}}{3} + x]_{0}^{2} - \frac{25}{8} = \frac{14}{3} - \frac{25}{8} = \frac{37}{24}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST 5 (2020)-MATHEMATICS (SECTION 2)

Home
Ask Doubt
Profile