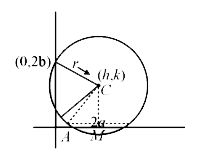
A circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distant 2b from the origin. Then the locus of the centre of this circle is
A parabola
A hyperbola
A straight line
An elipse
The correct Answer is:A
In ΔACM:
K2+4a2=r2 …(i)
h2+(K−2b)2=r2 …(ii)
K2+4a2=h2+(K−2b)2
K2+4a2=h2+K2+4b2−4Kb
∴h2=4Kb+4a2−4b2
x2=4by+4a2−4b2
∴ Parabola.
Topper's Solved these Questions
- JEE MAIN REVISION TEST 5 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 5 (2020)EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST 11 (2020) BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 11 (2020) EXERCISE - MATHEMATICS (SECTION - 2)
4 Videos
- JEE MAIN REVISION TEST 8 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 8 (2020)EXERCISE - MATHEMATICS ( SECTION 2 )
5 Videos
Similar Questions
Prove that the locus of the center of a circle, which intercepts a chord of given length 2a on the axis of x and passes through a given point on the axis of y distant b from the origin, is a parabola.
View SolutionFind the equations of the circles passing through two points on y-axis at distance 3 from the origin and having radius 5.
View Solution
Knowledge Check
The smallest circle with centre on y-axis and passing through the point (7,3) has radius
A√58B7C3D4
The equation of the circle whose radius is 5 and which passes through the points on x-axis at a distance 3 from the origin is
View SolutionA circle cuts the chord on x-axis of length 4a. If this circle cuts the y-axis at a point whose distance from origin is 2b. Locus of its centre is (A) Ellipse (B) Parabola (C) Hyperbola (D) Straight line
View SolutionFind the equation of the circle which passes through two points on the x-axis which are at distances 4 from the origin and whose radius is 5.
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is
View SolutionA line is at a distance c from origin and meets axes in A and B. The locus of the centre of the circle passing through O,A,B is
View SolutionIf a circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally then the locus of its centre is
View Solution
