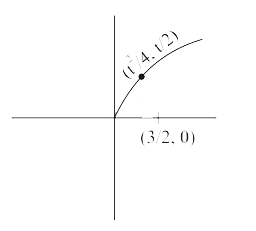
The shortest distance between the point (32,0) and the curve y=√x,(x>0)is
The correct Answer is:5
The point located nearest to the given point must be the point common to the parabola and the normal passing through (32,0).
t2t24−32=−t
2tt2−6+t=0
t(2t2−6+1)=0
t2−6=−2
t2=4
t=2 (t>0)
Point (1,1)
Distance =√(1−32)2+1=√52
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 29 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 29 (2020)Exercise:MATHEMATICS
Explore 25 Videos
- JEE MAIN REVISION TEST - 7|JEE - 2020Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 7|JEE - 2020Exercise:Mathematics (Section - 2) Numercial type questions
Explore 5 Videos
Similar Questions
The shortest distance between the point (32,0) and the curve y=√x,(x>0), is
View SolutionThe shortest distance between the point (0,12) and the curve x=√y,(y>0) , is:
View SolutionThe shortest distance between the line x=y and the curve y2=x−2 is
View SolutionFind the distance between the points (3,6) and (0,2)
View SolutionFind the distance between the points (0,0) and (3,4)
View SolutionFind the distance between the points (0,−3) and (3,0)
View SolutionIf each ai>0, then the shortest distance between the points (0,−3) and the curve y=1+a1x2+a2x4+.......+anx2n is
View SolutionFind the shortest distance between the line x−y+1=0 and the curve y2=x.
View SolutionFind the shortest distance between the line y=x−2 and the parabola y=x2+3x+2
View SolutionFind the distance between the point (0,3,0) and the plane 2x + y + 2x - 5
View Solution

