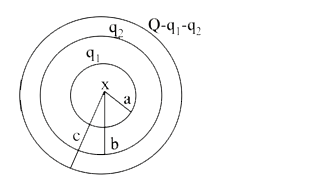
A charge Q is distributed over three concentric spherical shells of radii a, b, c (a $<$ b $<$ c) such that their surface charge densities are equal to one another.
The total potential at a point at distance r from their common centre, where r $<$ a, would be :

A

$\frac{Q (a + b + c)}{4 π ε_{0} (a^{2} + b^{2} c^{2})}$

B

$\frac{Q}{4 π ε_{0} (a + b + c)}$

C

$\frac{Q}{12 π ε_{0}} \frac{a b + b c + c a}{a b c}$

D

$\frac{Q (a^{2} + b^{2} + c^{2})}{4 π ε_{0} (a^{3} + b^{3} c^{3})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$\frac{q_{1}}{a^{2}} = \frac{q_{2}}{b^{2}} = \frac{Q - q_{1} - q_{2}}{C^{2}}$
$(q_{1}) = \frac{a^{2}}{b^{2}} q_{2}$
$q_{2} = \frac{b^{2}}{C^{2}} Q - \frac{b^{2}}{C^{2}} q_{1} - \frac{b^{2}}{C^{2}} q_{2}$
$\Rightarrow q_{2} (1 + \frac{b^{2}}{C^{2}}) = \frac{b^{2}}{C^{2}} Q - \frac{b^{2}}{C^{2}} q_{1}$
$\Rightarrow \frac{b^{2}}{a^{2}} q_{1} (1 + \frac{b^{2}}{C^{2}}) = \frac{b^{2}}{C^{2}} Q - \frac{b^{2}}{C^{2}} q_{1}$
$\Rightarrow (\frac{b^{2}}{a^{2}} + \frac{b^{4}}{a^{2} c^{2}}) q_{1} + \frac{b^{2}}{C^{2}} q_{1} = \frac{b^{2}}{C^{2}} Q$
$\Rightarrow \frac{b^{2}}{a^{2}} q_{1} (1 + \frac{b^{2}}{C^{2}} + \frac{a^{2}}{C^{2}}) = \frac{b^{2}}{C^{2}} Q$
$q_{1} = \frac{\frac{a^{2}}{C^{2}} Q}{\frac{C^{2} + b^{2} + a^{2}}{C^{2}}}$
$q_{1} \frac{a^{2}}{a^{2} + b^{2} + c^{2}} Q$
$q_{2} = \frac{b^{2}}{a^{2} + b^{2} c^{2}} Q$
$Q - q_{1} - q_{2} = \frac{c^{2}}{a^{2} + b^{2} + c^{2}} Q$
$V = \frac{k q_{1}}{a} + \frac{k q_{2}}{b} + \frac{k (Q - q_{1} - q_{2})}{C}$
$= \frac{Q}{4 π ε_{0}} [\frac{a}{a^{2} + b^{2} + c^{2}} + \frac{b}{a^{2} + b^{2} + c^{2}} + \frac{c}{a^{2} + b^{2} + c^{2}}] = \frac{Q}{4 π ε_{0}} (\frac{a + b + c}{a^{2} + b^{2} + c^{2}})$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST - 4 JEE - 2020-PHYSICS

Home
Ask Doubt
Profile