The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5 ) that fuse after 200 days of use . Find the probability of
(i)X=0,(ii)X≤1,(iii)X>1,(iv)X≥1.
The correct Answer is:i)(0.8)5ii)1.8×(0.8)4iii)1–(0.8)5iv)1−1.8×(0.8)4
To solve the problem, we will use the binomial probability formula, which is given by:
P(X=k)=(nk)pkqn−k
where:
- n is the total number of trials (in this case, 5 bulbs),
- k is the number of successes (bulbs that fuse),
- p is the probability of success (bulb fuses),
- q is the probability of failure (bulb does not fuse).
Given:
- p=0.2 (probability that a bulb fuses),
- q=1−p=0.8 (probability that a bulb does not fuse),
- n=5 (total number of bulbs).
Now, we will find the probabilities for each part of the question:
(i) Find P(X=0)
Using the binomial formula:
P(X=0)=(50)(0.2)0(0.8)5=1⋅1⋅(0.8)5
Calculating (0.8)5:
(0.8)5=0.32768
Thus,
P(X=0)=0.32768
(ii) Find P(X≤1)
This is the sum of the probabilities for X=0 and X=1:
P(X≤1)=P(X=0)+P(X=1)
We already calculated P(X=0). Now we calculate P(X=1):
P(X=1)=(51)(0.2)1(0.8)4=5⋅(0.2)⋅(0.8)4
Calculating (0.8)4:
(0.8)4=0.4096
Thus,
P(X=1)=5⋅0.2⋅0.4096=5⋅0.08192=0.4096
Now, adding both probabilities:
P(X≤1)=0.32768+0.4096=0.73728
(iii) Find P(X>1)
This can be calculated as:
P(X>1)=1−P(X≤1)
Thus,
P(X>1)=1−0.73728=0.26272
(iv) Find P(X≥1)
This can be calculated as:
P(X≥1)=1−P(X=0)
Thus,
P(X≥1)=1−0.32768=0.67232
Summary of Results:
- P(X=0)=0.32768
- P(X≤1)=0.73728
- P(X>1)=0.26272
- P(X≥1)=0.67232
- n is the total number of trials (in this case, 5 bulbs),
- k is the number of successes (bulbs that fuse),
- p is the probability of success (bulb fuses),
- q is the probability of failure (bulb does not fuse).
- p=0.2 (probability that a bulb fuses),
- q=1−p=0.8 (probability that a bulb does not fuse),
- n=5 (total number of bulbs).
- P(X=0)=0.32768
- P(X≤1)=0.73728
- P(X>1)=0.26272
- P(X≥1)=0.67232
Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II PROBABILITY DISTRIBUTIONS (ACTIVITIES)
Explore 5 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:MATHEMATICAL LOGIC
Explore 32 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II PROBABILITY DISTRIBUTIONS (III. State whether each of the following is True or False.)
Explore 9 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
The probability that a bulb produced by a factory will fuse after 160 days of use is 0.06. Find the probability that out of 5 such bulbs at the most one bulb will fuse after 160 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after an year of use is 0.1. Then the probability that out of 4 such bulbs, only one is working after an year
View Solution
Knowledge Check
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs none will fuse after 150 days of use?
A1−(1920)5B(1920)5C(34)5D90(14)5The probability that tulb produced by a factor will fuse after 150 days if used is 0.50. What is the probability that out of 5 such balbs none will fuse after 150 days of use ?
A1−(19/20)5B(19/20)5C(3/4)5D90(1/4)5
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs :
(i) none
(ii) none more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 6 months of use is 0.05 . Find the probability that out of 5 such bulbs
(i) none will fuse after 6 months of use
(ii) at least one will fuse after 6 months of use
(iii) not more than one will fuse after 6 months of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs(i) none(ii) not more than one(iii) more than one(iv) at least onewill fuse after 150 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days if used is 0.05. what is the probability that out of 5 such bulbs none will fuse after 150 days of use? 1−(1920)5 b. (1920)5 c. (34)5 d. 90(14)5
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. If a sample of such 5 bulbs are taken out, then match the probabilities in column I with their respective values in column II and choose the correct option from the codes given below.
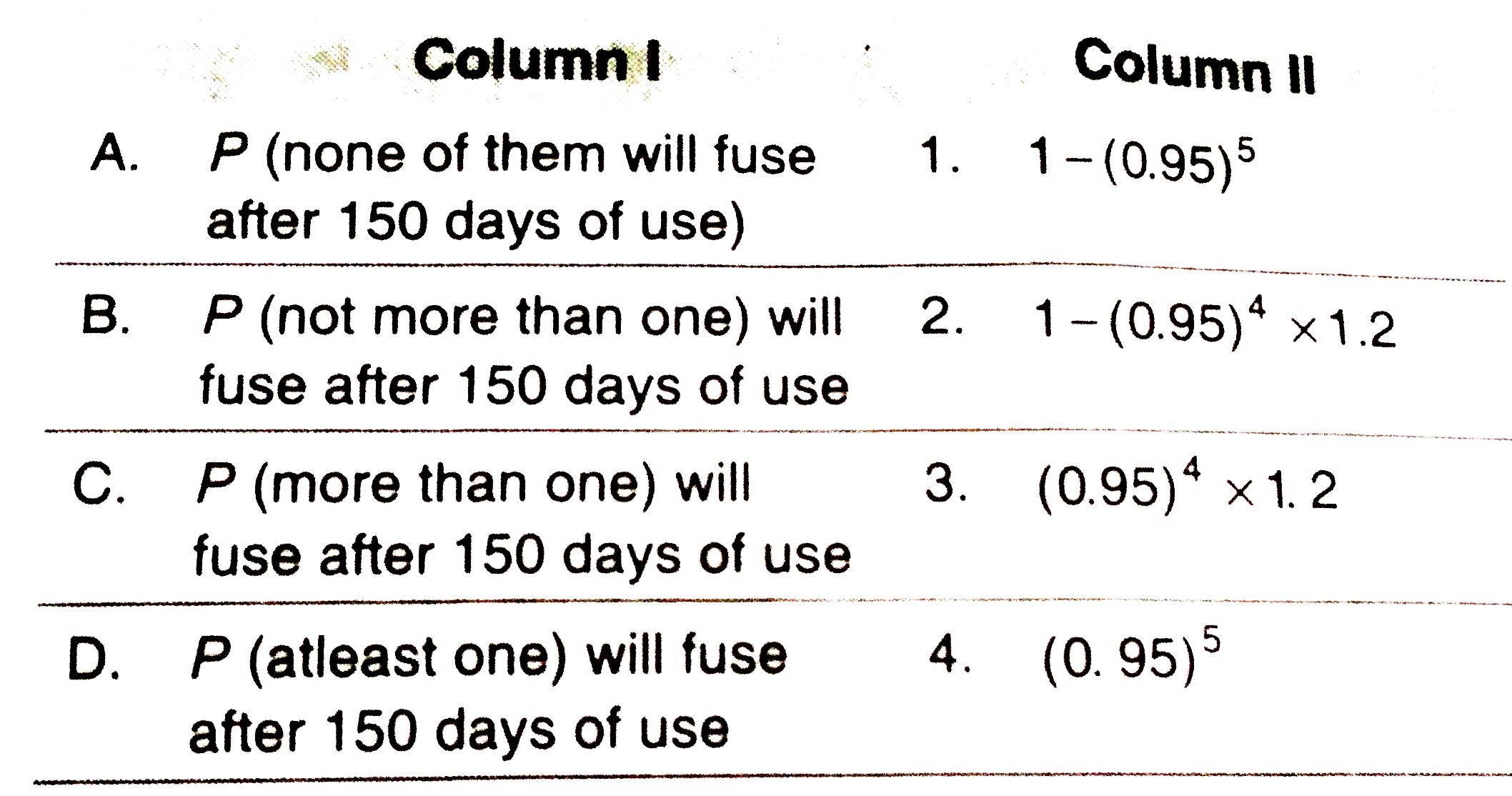
View SolutionFind tha values of x2 for the given values of x. (i) x<2
(ii) x>−1
(iii) x≥2
(iv) x<−1
View Solution

