If a r. v. X assumes the values 1,2,3,…………,9 with equal probabilities then E(x) = 5.
The correct Answer is:True
Step by step video, text & image solution for If a r. v. X assumes the values 1,2,3,…………,9 with equal probabilities then E(x) = 5. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (Solve the following)
17 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (ACTIVITIES)
5 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (II. Fill in the blanks)
7 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
A random variable X takes values 0,1,2,...... with probability proportional to (x with proba bility proportional to (x+1)(15)x, , then 5⋅[P(x≤1)12] equals
View SolutionLet [x] denote the greatest integer less than or equal to x. Then, the values of x∈R satisfying the equation [ex]2+[ex+1]−3=0
View Solution
Knowledge Check
A r.v. X assumes values 1, 2, 3, …, n with equal probabilities. If Var (X) = E (X), then n =
A11B5C6D7A r.v. X assumes values 1, 2, 3, …, n with equal probabilities. If Var (X) = 4 E (X), then n =
A49B23C25D24A random variable X takes values 0, 1, 2, 3,… with probability proportional to (x+1)(15)x.
P(X≥2) equalsA1125B1325C11125D13125
Let X be a random variable which assumes values x1,x2,x3, x4 such that 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4). Find the probability distribution of X.
View SolutionIf a c.r.v. X has the probability density function
f(x)=C(9−x2),0<x<3
= 0 , otherwise
Then, the value of C is
View SolutionThe value of ∫10ex2xdx is equal to:
View SolutionFor the following probability distribution.
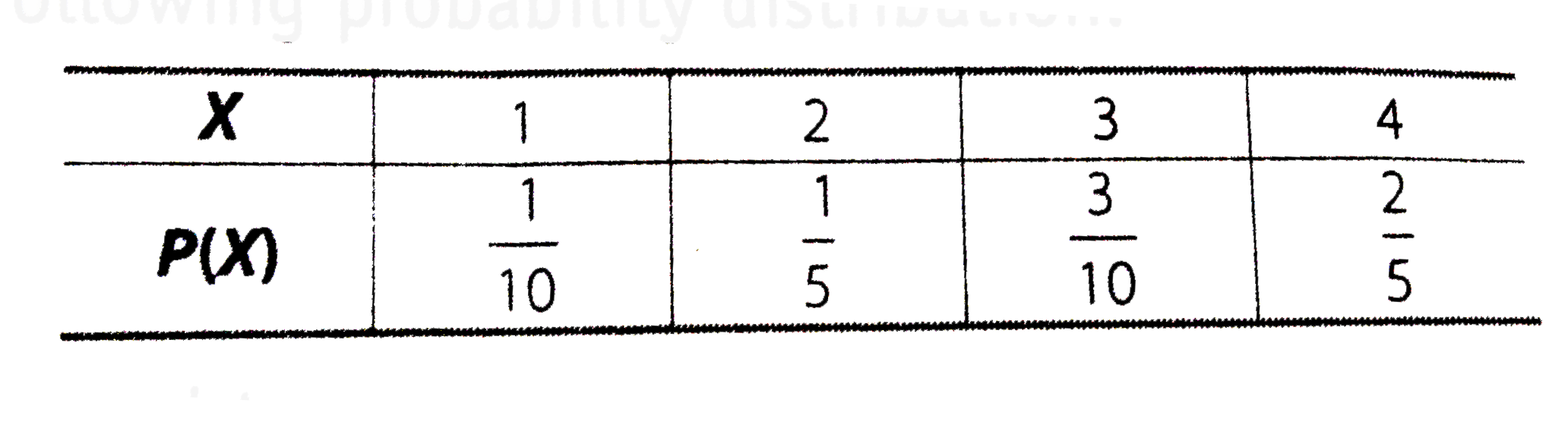
E(X2) is equal to
View SolutionThe p.m.f. of a r.v. X is
P(x) =1/15, for x =1,2, .......... , 14,15
= 0 otherwise.
Then, E(X) is equal to
View Solution
