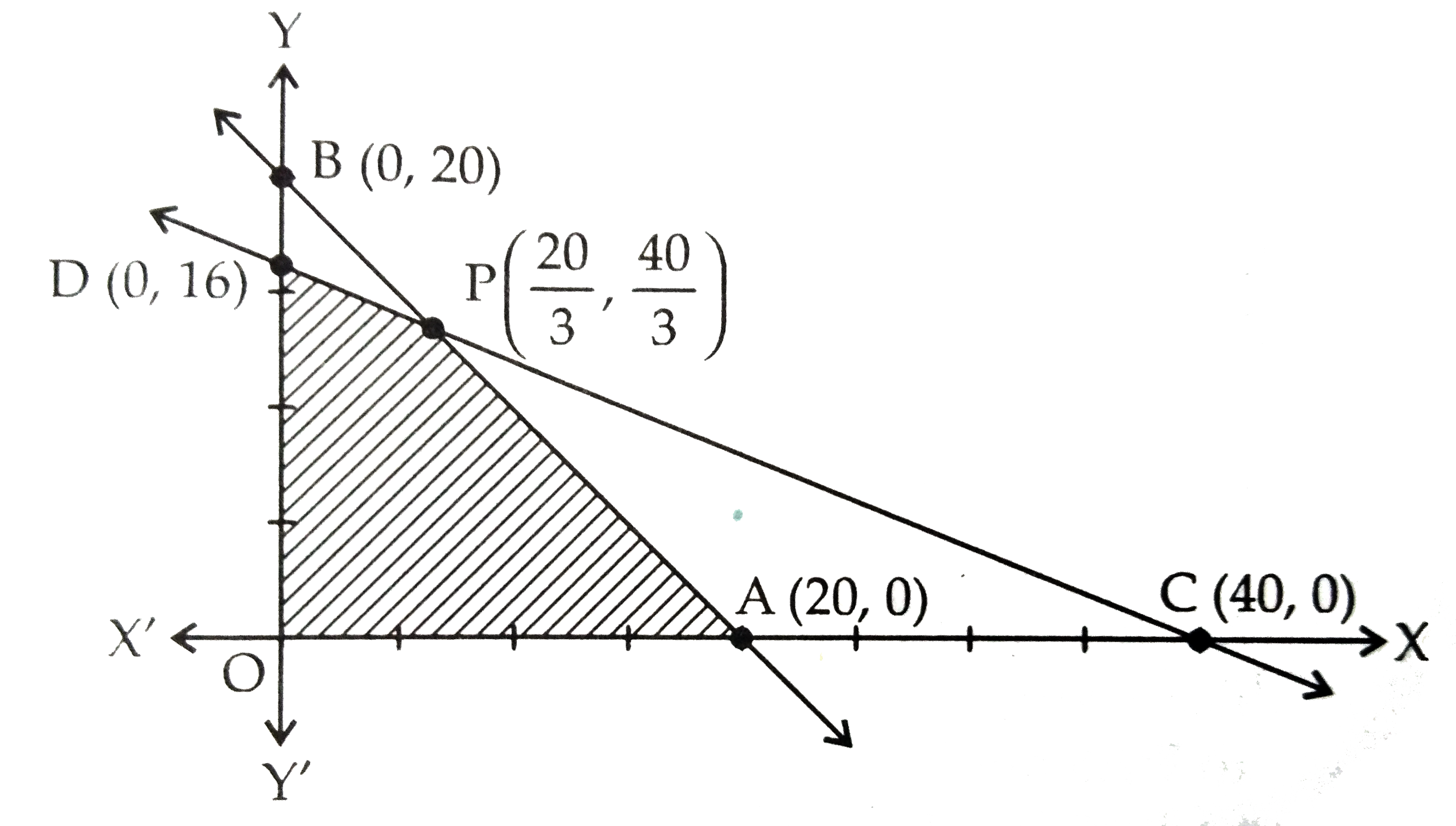
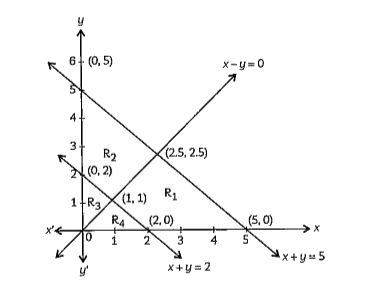
The feasible region is the set of point which satisfy
common region determined by all the constraints
common region determined by the non-negativity constraints
either of the options a or b
either of the options a or b
The correct Answer is:D
Step by step video, text & image solution for The feasible region is the set of point which satisfy by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (B. State whether each of the following statement is TRUE or FALSE)
12 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (C. Fill in each of the following blanks)
12 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 5. INDEX NUMBERS (V Activity)
1 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
The region M consists of all the points (x, y) satisfying the inequalities y≥0,y≤x and y≤2−x. The region N which varies with the parameter t consists of all points which satisfy t≤x≤t+1∀t∈[0,1], then min(ar(M ∩ N)) is
A12 sq. unitsB34 sq. unitsC78 unitsD163 sq. unitsThe corner point method for bounded feasible region comprises of the following steps
I. When the feasible region is bounded, M and m are the maximum and minimum values of Z.
II. Find the feasible region of the linear programming problem and determine its corner points.
Ill. Evaluate the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values of these points.
The correct order of these above steps isAIII,I,IIBII,III,ICII,I,IIIDI,III,IIIn the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
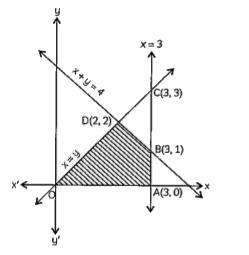 AOBBCCDD
AOBBCCDD
A corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum?
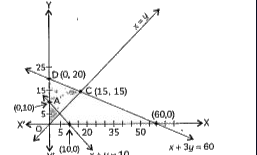
View SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z=3x+9y maximum?
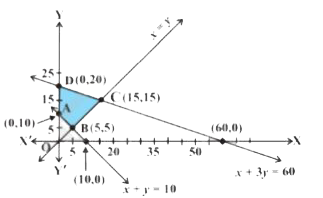
View SolutionDefine the feasible region.
View SolutionConsider the following LPP:
Maximize Z=3x+2y subject to the constraints:
x+2y≤10,3x+y≤15,x,y≥0.
(a) Draw the feasible region.
(b)Find the corner points of the feasible region.
(c) Find the maximum value of Z.
View Solution