AB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and AB∣∣CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
The correct Answer is:3
The x-component of velocity remains same while the y-component of velocity is halved and gets reversed.
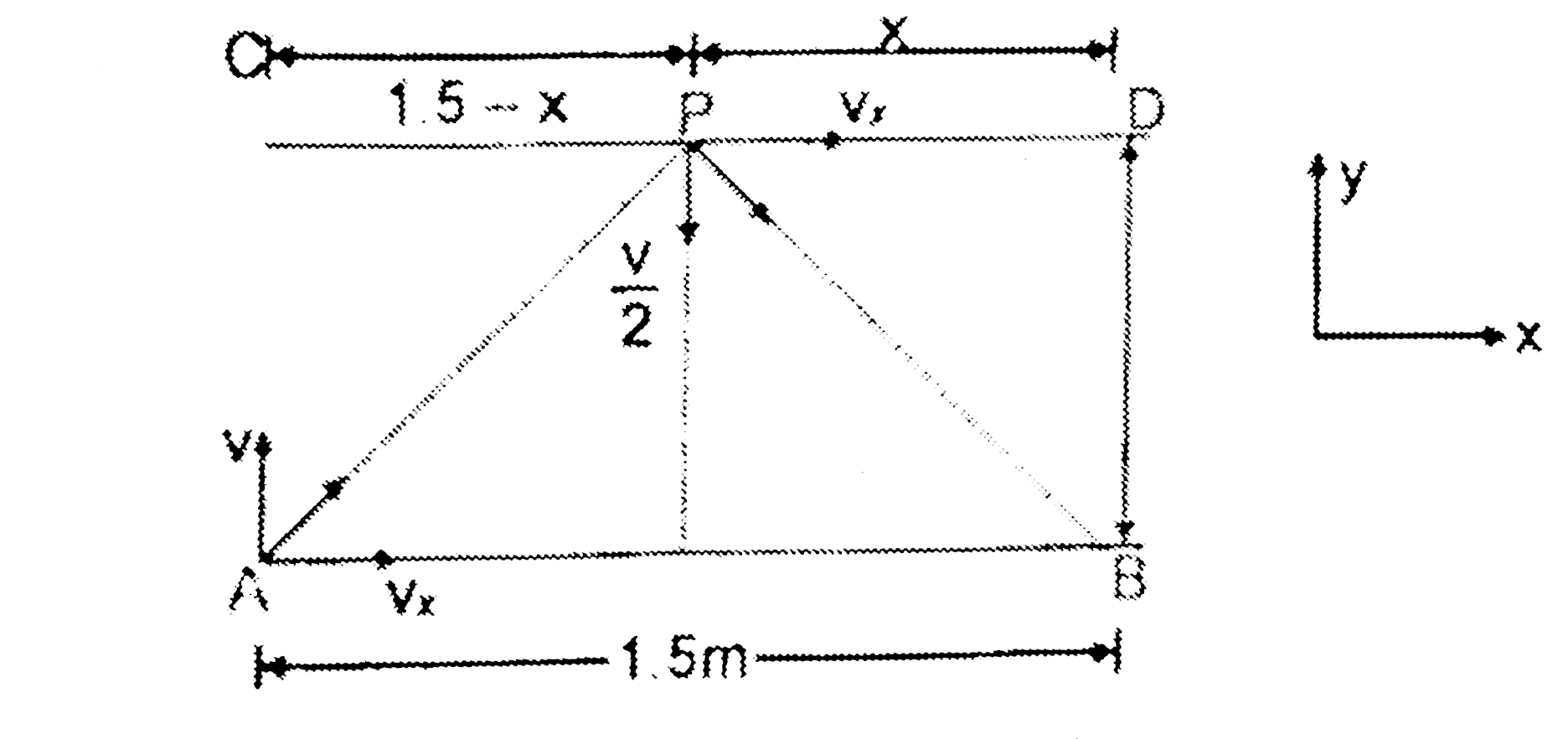
so, the ball will cover twice the distance in x-direct compare to before collision
As we use x=2(1.5−x)
x=3−2x
3x=3
x=1m
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - CHEMISTRY24videos
TEST PAPER
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - MATHEMATICS48videos
TEST PAPER
- BOOK - RESONANCE ENGLISHCHAPTER - SEQUENCE & SERIES EXERCISE - EXERCISE -2 (PART-II : PREVIOUSLY ASKED QUESTION OF RMO)3videos
SEQUENCE & SERIES
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS259videos
TEST PAPERS
Similar Questions
AB and CD are two chords of a circle such that AB=6cm,CD=12cm and AB∣∣CD. If the distance between AB and CD is 3cm , find the radius of the circle.
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm If the distance between ABandCD is 3cm find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is (a)6 cm (b) 5 √2 cm (c) 7 cm (d) 3 √5 cm
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD.
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=X cm, and distance between AB and DC is 4cm . Find the value of X and area of trapezium ABCD
View SolutionAC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters
(ii) ABCD is a rectangleView SolutionDraw a parallelogram ABCD in which AB=8cm, AD=5cm and ∠A=600.
View Solution
