From the matrix equation AB=AC, we conclude B=C provided.
A is singular
A is non-singular
A is symmetric
A is a square
The correct Answer is:B
To solve the problem, we need to analyze the matrix equation AB=AC and determine under what conditions we can conclude that B=C.
1. Start with the given equation:
AB=AC
2. Subtract AC from both sides:
AB−AC=0
3. Factor out A from the left-hand side:
A(B−C)=0
4. Analyze the product A(B−C)=0:
This equation states that the product of matrix A and the matrix (B−C) equals the zero matrix.
5. Consider the implications of this product being zero:
For the equation A(B−C)=0 to imply B−C=0 (or B=C), A must be a non-singular matrix. A non-singular matrix is one that has an inverse, which means its determinant is non-zero.
6. Multiply both sides by A−1 (the inverse of A):
A−1(A(B−C))=A−10
This simplifies to:
I(B−C)=0
where I is the identity matrix.
7. Conclude that:
B−C=0⇒B=C
Conclusion:
Thus, we conclude that B=C provided that A is a non-singular matrix (i.e., det(A)≠0).
AB=AC
AB−AC=0
A(B−C)=0
This equation states that the product of matrix A and the matrix (B−C) equals the zero matrix.
For the equation A(B−C)=0 to imply B−C=0 (or B=C), A must be a non-singular matrix. A non-singular matrix is one that has an inverse, which means its determinant is non-zero.
A−1(A(B−C))=A−10
This simplifies to:
I(B−C)=0
where I is the identity matrix.
B−C=0⇒B=C
Thus, we conclude that B=C provided that A is a non-singular matrix (i.e., det(A)≠0).
Topper's Solved these Questions
- MATRICES & DETERMINANTBOOK - RESONANCE ENGLISHCHAPTER - MATRICES & DETERMINANTEXERCISE - PART-III
18 Videos
- MATRICES & DETERMINANTBOOK - RESONANCE ENGLISHCHAPTER - MATRICES & DETERMINANTEXERCISE - PART-IV
1 Video
- MATRICES & DETERMINANTBOOK - RESONANCE ENGLISHCHAPTER - MATRICES & DETERMINANTEXERCISE - PART-II
26 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCE ENGLISHCHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
- NUMBER THEORYBOOK - RESONANCE ENGLISHCHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4 Videos
Similar Questions
Knowledge Check
From the passage, we can conclude that:
ANew ventures are not risky.BNew ventures are inherently risky.CFinancial investment in a new venture is always non-profitable.DConservative projection of companies' profits is suggestedIf the order of the matrix A is m×n and the order of the matrix B is n×p, then the order of matrix A.B is:
Am×nBn×pCm×pDp×p
If A, B, and C are three square matrices of the same order, then AB=AC⇒B=C. Then
View SolutionIf A∩B=A∪B then what can we conclude ?
View SolutionIn a parallelogram as shown in the figure (a≠b)
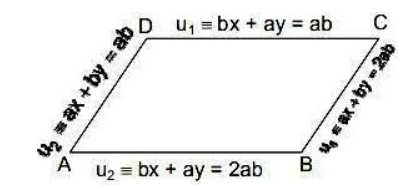
Prove that the equation of the diagonal AC is (a+b)x+(a+b)y=3ab
View SolutionIn a △ABC , B=(2,3),C=(7,-1) and AB=3,AC=5 then find the equation of altitude through the vertex A.
View SolutionLet A be an orthogonal matrix, and B is a matrix such that AB=BA, then show that ABT=BTA.
View SolutionIf A is matrix of order m×n and B is a matrix such that AB' and B'A are both defined , then order of matrix B is
View Solution

_E01_054_Q01.png)