A dipole is formed by two point charge -q and +q, each of mass m, and both the point charge are connected by a rod of length and mass m. This dipole is placed in uniform electric field If the dipole is disturbed by a small angle from stable equilibrium position, prove that its motion will be almost SHM. also find its time period.
To solve the problem step by step, we will analyze the behavior of a dipole in a uniform electric field when it is disturbed from its equilibrium position.
Step 1: Understanding the Dipole in an Electric Field
A dipole consists of two equal and opposite charges, -q and +q, separated by a distance l. The dipole moment \( \vec{P} \) is given by:
\(
\vec{P} = q \cdot \vec{l}
\)
where \( \vec{l} \) is a vector pointing from the negative charge to the positive charge.
Step 2: Torque on the Dipole
When the dipole is placed in a uniform electric field \( \vec{E} \), it experiences a torque \( \tau \) given by:
\(
\tau = \vec{P} \times \vec{E} = P E \sin \theta
\)
where \( \theta \) is the angle between the dipole moment and the electric field.
Step 3: Equation of Motion
The torque causes an angular acceleration \( \alpha \) of the dipole. According to Newton's second law for rotation, we have:
\(
\tau = I \alpha
\)
where \( I \) is the moment of inertia of the dipole about the axis of rotation. Thus,
\(
I \alpha = -P E \sin \theta
\)
The negative sign indicates that the torque acts in the opposite direction of the displacement from equilibrium.
Step 4: Small Angle Approximation
For small angles \( \theta \), we can use the approximation:
\(
\sin \theta \approx \theta
\)
Substituting this into the equation gives:
\(
I \frac{d^2 \theta}{dt^2} = -P E \theta
\)
Step 5: Form of the Equation
Rearranging this equation, we have:
\(
\frac{d^2 \theta}{dt^2} + \frac{P E}{I} \theta = 0
\)
This is the standard form of the simple harmonic motion (SHM) equation, where:
\(
\omega^2 = \frac{P E}{I}
\)
Step 6: Time Period of the Motion
The time period \( T \) of the SHM can be expressed as:
\(
T = 2\pi \sqrt{\frac{I}{P E}}
\)
Summary
We have shown that the motion of the dipole, when disturbed from its equilibrium position, behaves like simple harmonic motion (SHM) for small angles. The time period of this motion is given by:
\(
T = 2\pi \sqrt{\frac{I}{P E}}
\)
A dipole consists of two equal and opposite charges, -q and +q, separated by a distance l. The dipole moment \( \vec{P} \) is given by:
\(
\vec{P} = q \cdot \vec{l}
\)
where \( \vec{l} \) is a vector pointing from the negative charge to the positive charge.
When the dipole is placed in a uniform electric field \( \vec{E} \), it experiences a torque \( \tau \) given by:
\(
\tau = \vec{P} \times \vec{E} = P E \sin \theta
\)
where \( \theta \) is the angle between the dipole moment and the electric field.
The torque causes an angular acceleration \( \alpha \) of the dipole. According to Newton's second law for rotation, we have:
\(
\tau = I \alpha
\)
where \( I \) is the moment of inertia of the dipole about the axis of rotation. Thus,
\(
I \alpha = -P E \sin \theta
\)
The negative sign indicates that the torque acts in the opposite direction of the displacement from equilibrium.
For small angles \( \theta \), we can use the approximation:
\(
\sin \theta \approx \theta
\)
Substituting this into the equation gives:
\(
I \frac{d^2 \theta}{dt^2} = -P E \theta
\)
Rearranging this equation, we have:
\(
\frac{d^2 \theta}{dt^2} + \frac{P E}{I} \theta = 0
\)
This is the standard form of the simple harmonic motion (SHM) equation, where:
\(
\omega^2 = \frac{P E}{I}
\)
The time period \( T \) of the SHM can be expressed as:
\(
T = 2\pi \sqrt{\frac{I}{P E}}
\)
We have shown that the motion of the dipole, when disturbed from its equilibrium position, behaves like simple harmonic motion (SHM) for small angles. The time period of this motion is given by:
\(
T = 2\pi \sqrt{\frac{I}{P E}}
\)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Two small balls A and B of positive charge Q each and masses m and 2m, respectively, are connected by a nonconducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
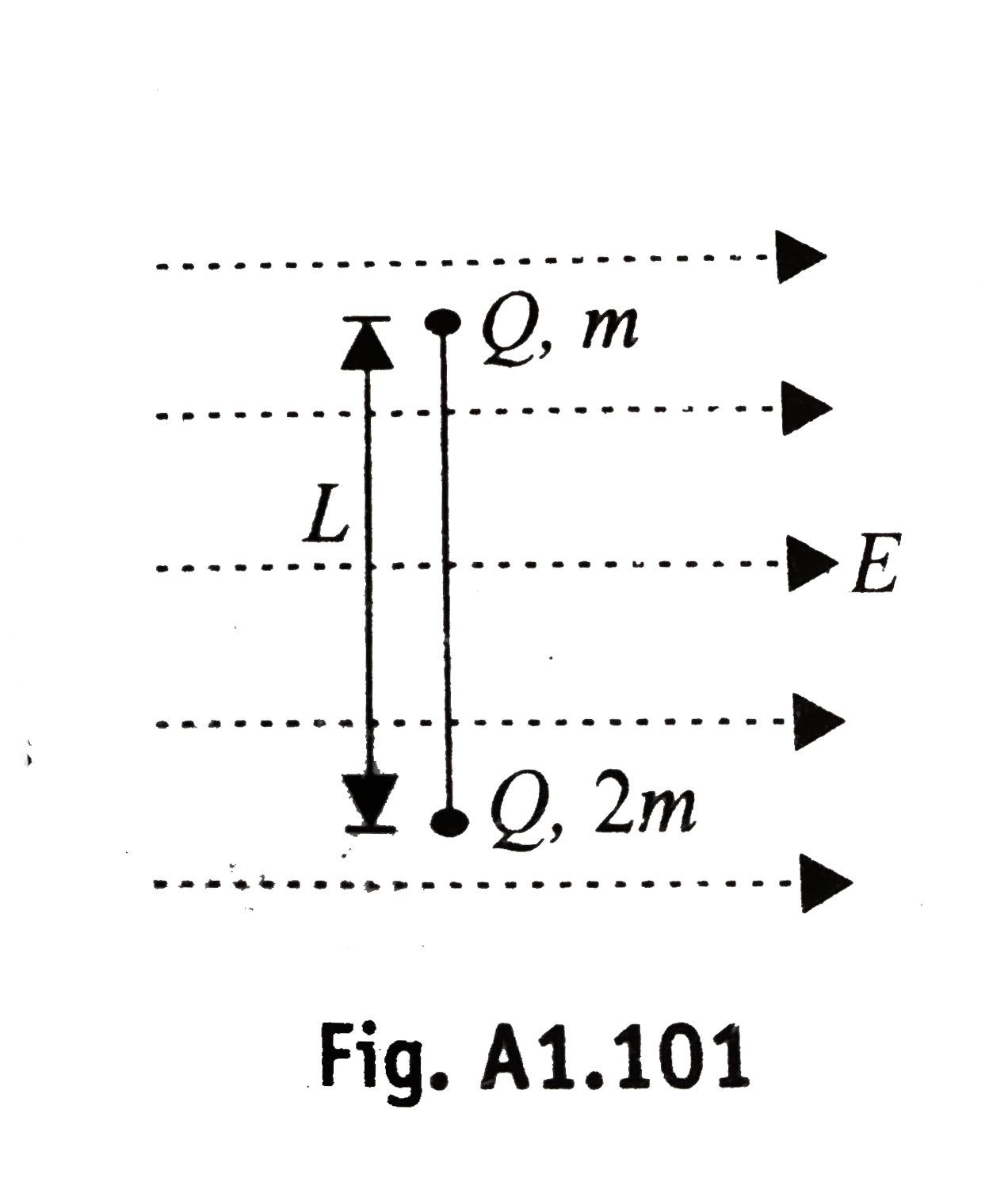
View Solutionshow an electric dipole formed by two
. particles fixed at the ends of a light rod of length l. The
. mass of each particle is m and the charges are -q and
. +q . The system is placed in such a way that the dipole
. axis is parallel to a uniform electric field E that exist
. in the region. The dipole is slightly rotated abut its
. centre and released. Show that for small angular
. displacement, the motion is anguler simple harmonic
. and find its time period.

View SolutionA electric dipole is in equilibrium having charge q and −q are placed at distance 'd' are placed at distance 'd' in a uniform electric filed E. Each charge has mass 'm'. If dipole is displaced by small angle. Then its angular frequency of oscillation.
View SolutionTwo point masses, m each carrying charges −q and +q are attached to the ends of a massless rigid non - conducting wire of length L. When this arrangement is placed in a uniform electric field, then it deflects through an angle θ. The minimum time needed by the rod to align itself along the field is
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View SolutionAn elastic dipole is formed by two equal and opposite charge with separation d. The charges have same mass m. It is Kept in a uniform electric field E. If it is slightly rotated from its equilibrium frequency ω is
View SolutionAn electric dipole is formed by two equal and opposite charges q with separation d. The charges have same mass m. It is kept in a uniform electric field E. If it is slightly rotated from its equilibrium orientation, then its angular frequency ω is:
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
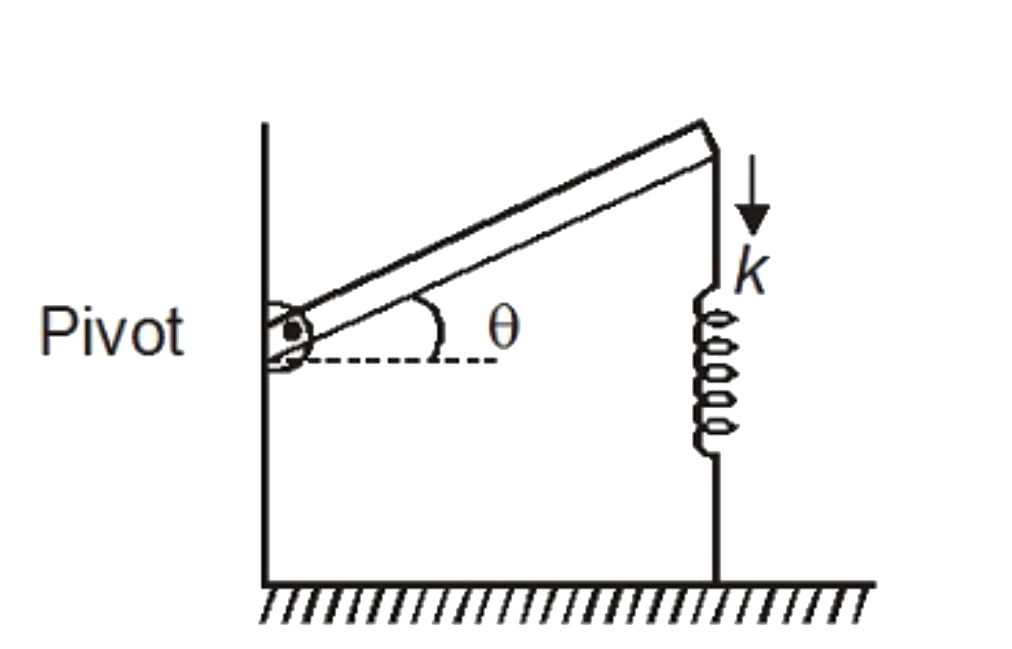
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View Solution
