Find out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
We can charge solid sphere to be made of large number of concentric spherical shells. Also electric field intensity at the location of any particular shell is constant.
∴Uinside=∫R012ε0E2dV
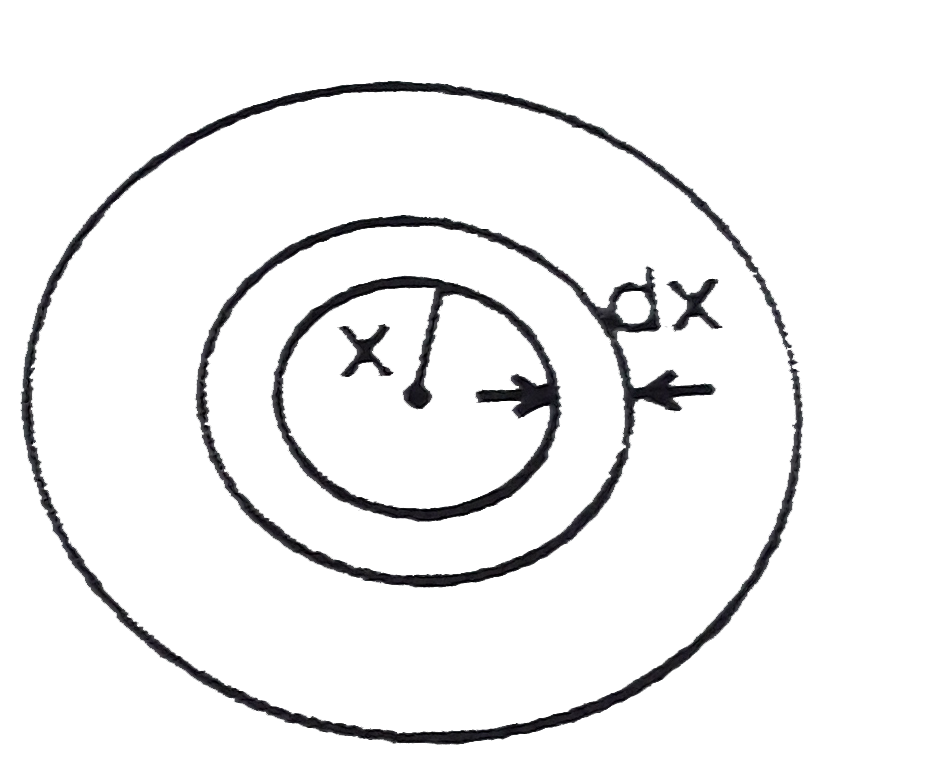
Consider an elementary shell of thickness dx and radius x.
Volume of the shell =(4πx2dx)
Uinside=∫R012ε0[KQxR3]2.4πx2dx=12ε0K2Q24πR6∫R0x4dx
=4πε02R6Q2(4πε0)2.R55=Q240πε0R=KQ210R.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Find the electric potential energy of a unifomly charged then spherical shell.
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionFind the electric potential energy of a uniformly charged sphere.
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionFind the energy stored in the electirc field produced by a metal sphere of radius R containing a charge Q.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charged sperical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r>Randr<R. (r being the distance from the centre of the shell)
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View Solution
