Find out energy stored in an imaginary cubical volume of side a in front of a infinitely large non-conducting sheet of uniform charge density σ.
To find the energy stored in an imaginary cubical volume of side a in front of an infinitely large non-conducting sheet of uniform charge density σ, we can follow these steps:
Step 1: Determine the Electric Field
The electric field E due to an infinitely large non-conducting sheet with uniform charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Step 2: Write the Expression for Energy Density
The energy density u (energy per unit volume) in an electric field is given by:
u=12ϵ0E2
Step 3: Substitute the Electric Field into the Energy Density Formula
Substituting the expression for E into the energy density formula:
u=12ϵ0(σ2ϵ0)2
Calculating this gives:
u=12ϵ0⋅σ24ϵ20=σ28ϵ0
Step 4: Calculate the Total Energy Stored in the Cube
The total energy U stored in the cubical volume can be found by multiplying the energy density by the volume of the cube. The volume V of the cube with side a is given by:
V=a3
Thus, the total energy stored is:
U=u⋅V=(σ28ϵ0)⋅a3
This simplifies to:
U=σ2a38ϵ0
Final Answer
The energy stored in the imaginary cubical volume of side a in front of the infinitely large non-conducting sheet is:
U=σ2a38ϵ0
---
The electric field E due to an infinitely large non-conducting sheet with uniform charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
The energy density u (energy per unit volume) in an electric field is given by:
u=12ϵ0E2
Substituting the expression for E into the energy density formula:
u=12ϵ0(σ2ϵ0)2
Calculating this gives:
u=12ϵ0⋅σ24ϵ20=σ28ϵ0
The total energy U stored in the cubical volume can be found by multiplying the energy density by the volume of the cube. The volume V of the cube with side a is given by:
V=a3
Thus, the total energy stored is:
U=u⋅V=(σ28ϵ0)⋅a3
This simplifies to:
U=σ2a38ϵ0
The energy stored in the imaginary cubical volume of side a in front of the infinitely large non-conducting sheet is:
U=σ2a38ϵ0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
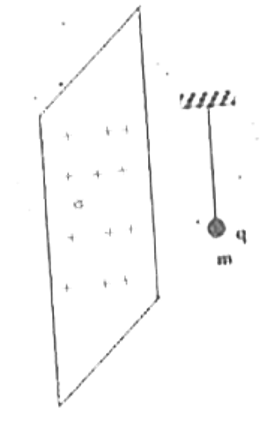
View SolutionA small charged particle of mass m and charge q is suspended by an insulated thread in front of a very large conducting charged sheet of uniform surface density of charge σ. The angle made by the thread with the vertical in equilibrium is
View SolutionDetermine and draw the graph of electric field due to infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ as a function of distance x from its symmetry plane.
(a) x<t2 (b) x≥t2
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
 .
.
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionFind out electric field intensity due to uniformly charged solid non-conducting sphere of volume charge density ρ and radius R at following points :
(i) At a distance r from surface of sphere (inside)
(ii) At a distance r from the surface of sphere (outside)
View SolutionIn a uniform electric field E if we consider an imaginary cubical closed surface of side a, then find the net flux through the cube ?
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

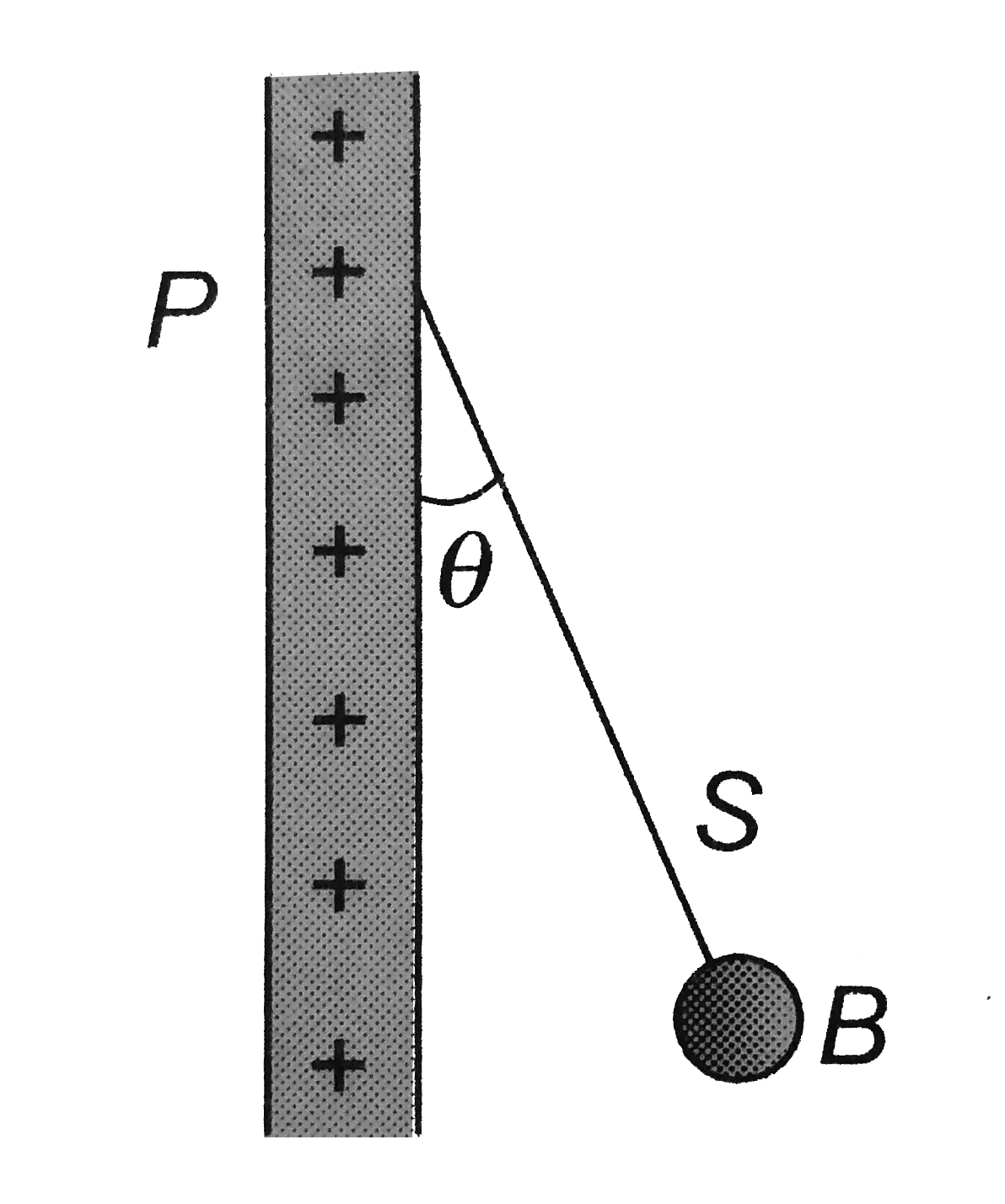
View SolutionA charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P, as shown in the figure. The surface charge density σ of the sheet is proportional to
View Solution
