Two hollow concentric non-conducting spheres of radius the a and contain charges and respectively. Prove that potential difference between the two spheres is independent of charge on outer sphere. If outer sphere is given an extra charge, is there any change in potential difference ?
To solve the problem, we need to analyze the potential difference between two hollow concentric non-conducting spheres with radii a (outer sphere) and b (inner sphere), having charges Qa and Qb respectively. Here’s a step-by-step solution:
Step 1: Understand the Configuration
We have two concentric non-conducting spheres:
- Sphere A (outer sphere) with radius a and charge Qa
- Sphere B (inner sphere) with radius b and charge Qb
Step 2: Calculate the Potential at the Surface of Sphere B
The potential VB at the surface of the inner sphere (radius b) is given by the formula for electric potential due to a point charge:
VB=kQbb+kQaa
where k is Coulomb's constant.
Step 3: Calculate the Potential at the Surface of Sphere A
The potential VA at the surface of the outer sphere (radius a) is given by:
VA=kQba+kQaa
Step 4: Calculate the Potential Difference
The potential difference ΔV between the two spheres is calculated as:
ΔV=VB−VA
Substituting the expressions for VB and VA:
ΔV=(kQbb+kQaa)−(kQba+kQaa)
This simplifies to:
ΔV=kQbb−kQba
ΔV=kQb(1b−1a)
Step 5: Analyze the Independence from Qa
Notice that the potential difference ΔV depends only on Qb and the radii a and b. The charge Qa does not appear in the final expression for ΔV, proving that the potential difference is independent of the charge on the outer sphere.
Step 6: Effect of Adding Extra Charge to the Outer Sphere
If we add an extra charge ΔQ to the outer sphere, the new charge becomes Qa+ΔQ. However, since the potential difference ΔV does not depend on Qa (as shown in the previous step), adding extra charge to the outer sphere does not change the potential difference.
Conclusion
Thus, we have shown that the potential difference between the two spheres is independent of the charge on the outer sphere, and adding extra charge to the outer sphere does not change the potential difference.
---
We have two concentric non-conducting spheres:
- Sphere A (outer sphere) with radius a and charge Qa
- Sphere B (inner sphere) with radius b and charge Qb
The potential VB at the surface of the inner sphere (radius b) is given by the formula for electric potential due to a point charge:
VB=kQbb+kQaa
where k is Coulomb's constant.
The potential VA at the surface of the outer sphere (radius a) is given by:
VA=kQba+kQaa
The potential difference ΔV between the two spheres is calculated as:
ΔV=VB−VA
Substituting the expressions for VB and VA:
ΔV=(kQbb+kQaa)−(kQba+kQaa)
This simplifies to:
ΔV=kQbb−kQba
ΔV=kQb(1b−1a)
Notice that the potential difference ΔV depends only on Qb and the radii a and b. The charge Qa does not appear in the final expression for ΔV, proving that the potential difference is independent of the charge on the outer sphere.
If we add an extra charge ΔQ to the outer sphere, the new charge becomes Qa+ΔQ. However, since the potential difference ΔV does not depend on Qa (as shown in the previous step), adding extra charge to the outer sphere does not change the potential difference.
Thus, we have shown that the potential difference between the two spheres is independent of the charge on the outer sphere, and adding extra charge to the outer sphere does not change the potential difference.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
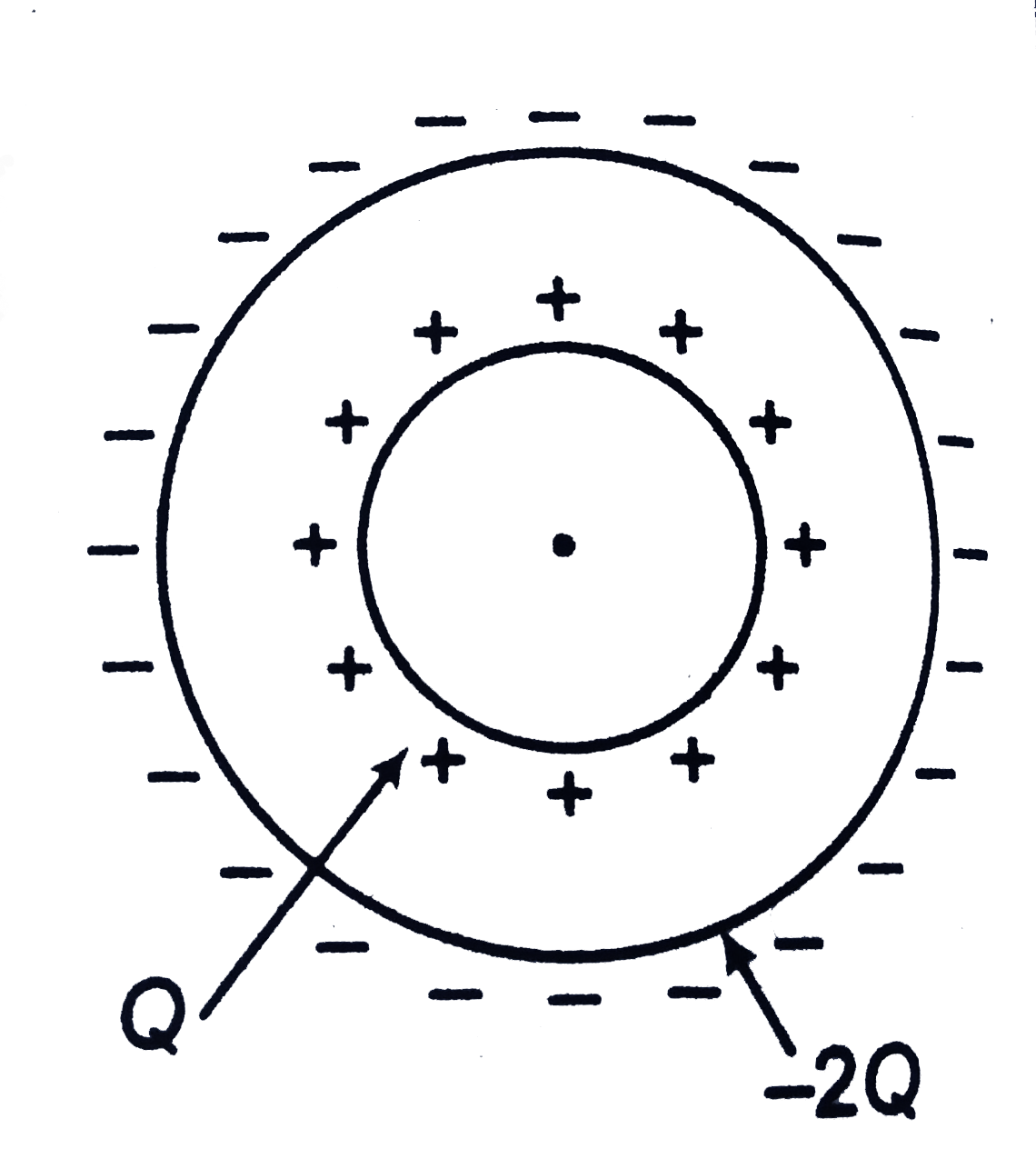
Two concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionTwo concentric hollow conducting spheres of radius a and b (b>a) contains charges Qa and Qb respectively. If they are connected by a conducting wire then find out following
(i) Final charges on inner and outer spheres.
(ii) Heat produced during the process.
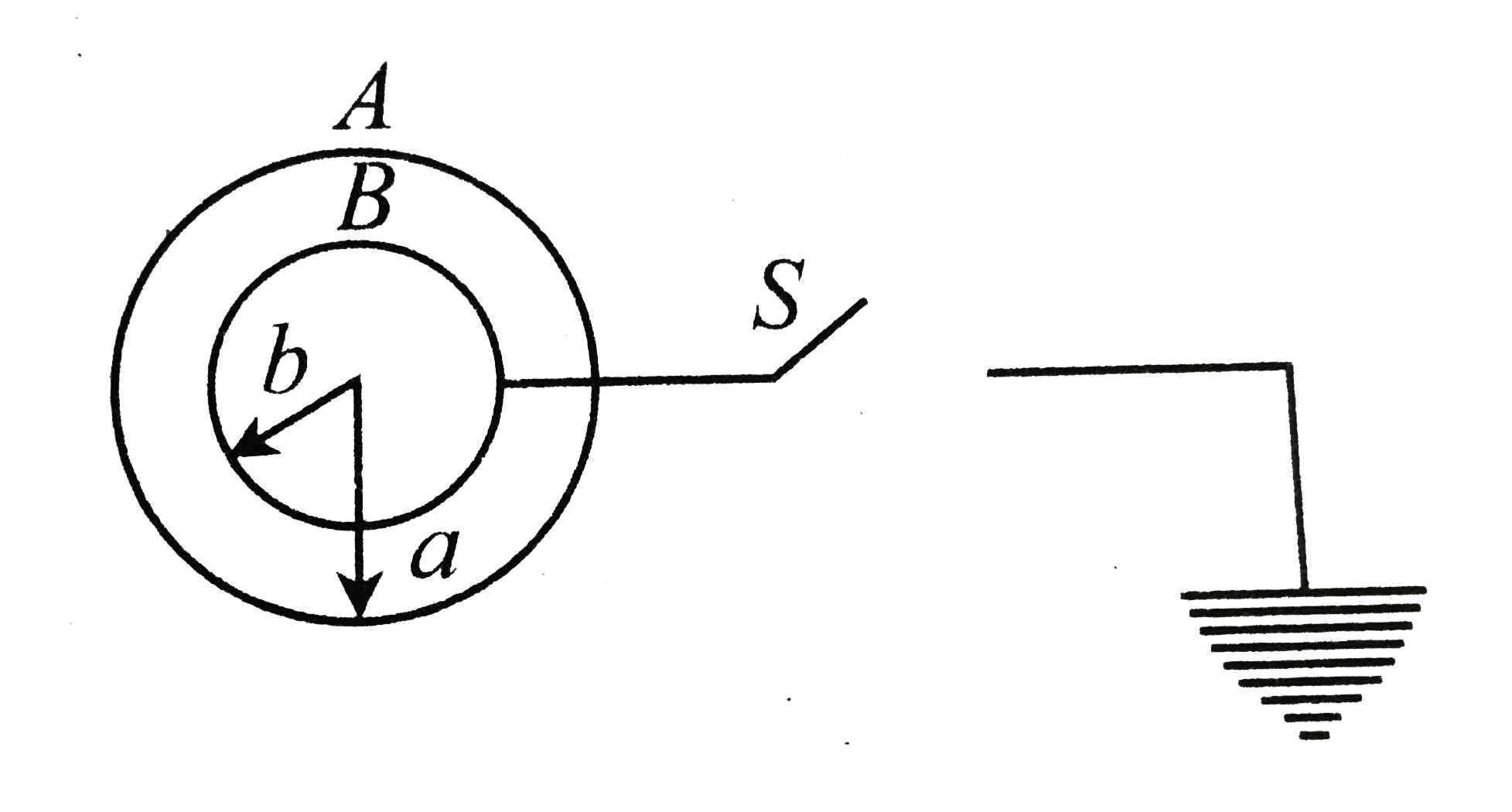
View SolutionConsider two concentric metal spheres. The outer sphere is given a charge Q>0, then
 ,
,
View SolutionA and B are two thin concentric hollow conductors having radii a and 2a and charge 2Q and Q, respectively. If potential of outer sphere is 5V, then potential of inner sphere is
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2.
Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionA solid conducting sphere, having a charge Q, is surrounded by an unchanged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a change of −4Q, the new potential difference between the same tow surface is :
View SolutionTwo non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.

View SolutionA conducting sphere is enclosed by a hollow conducting shell. Initially the inner sphere has a charge Q while the outer one is uncharged. The potential difference between the two spherical surface is found to be V. later on the outer shell is given a charge -4Q. The new potential difference between the two surfaces is : (A) V (B) −V (C) −2V (D) 2V
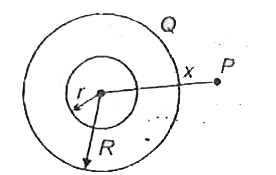
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
View Solution