Find the emf and internal resistance of a single battery which is equivalent to a combination of three batteries as show in figure.
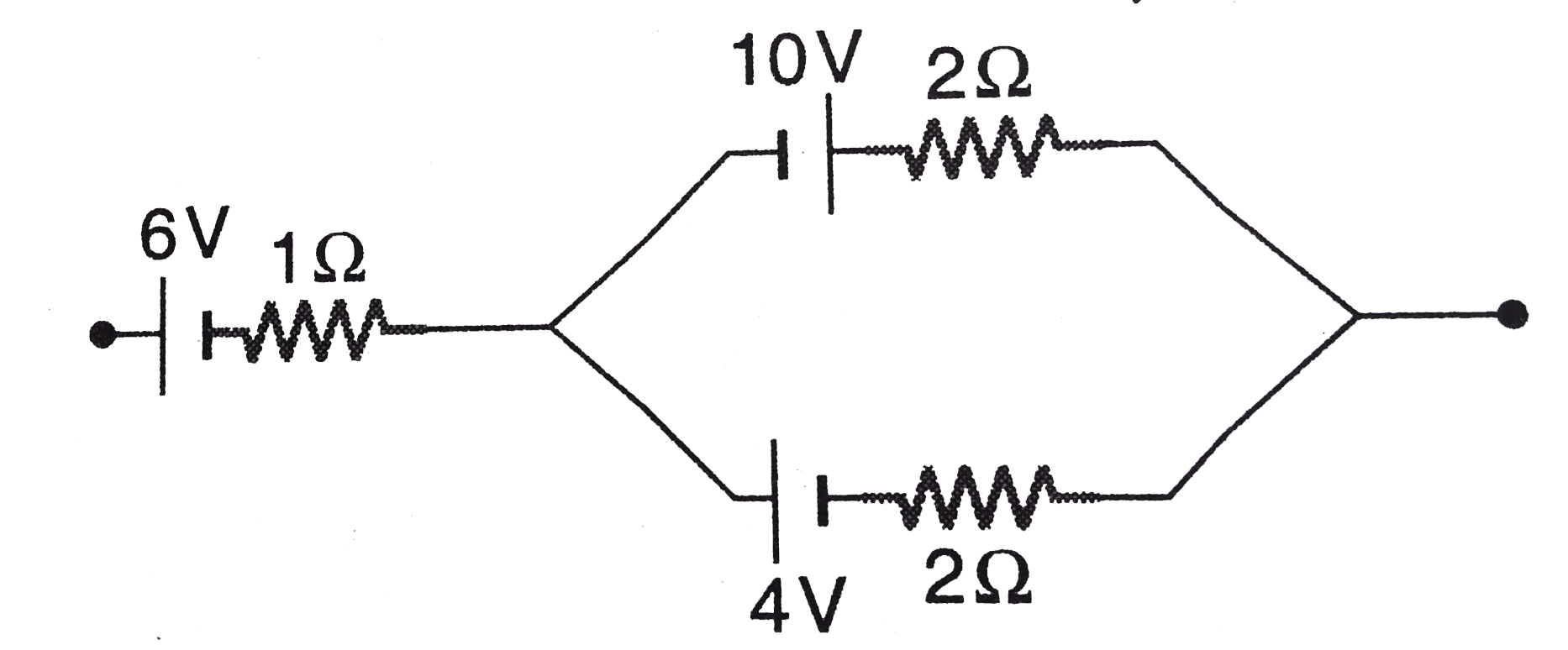
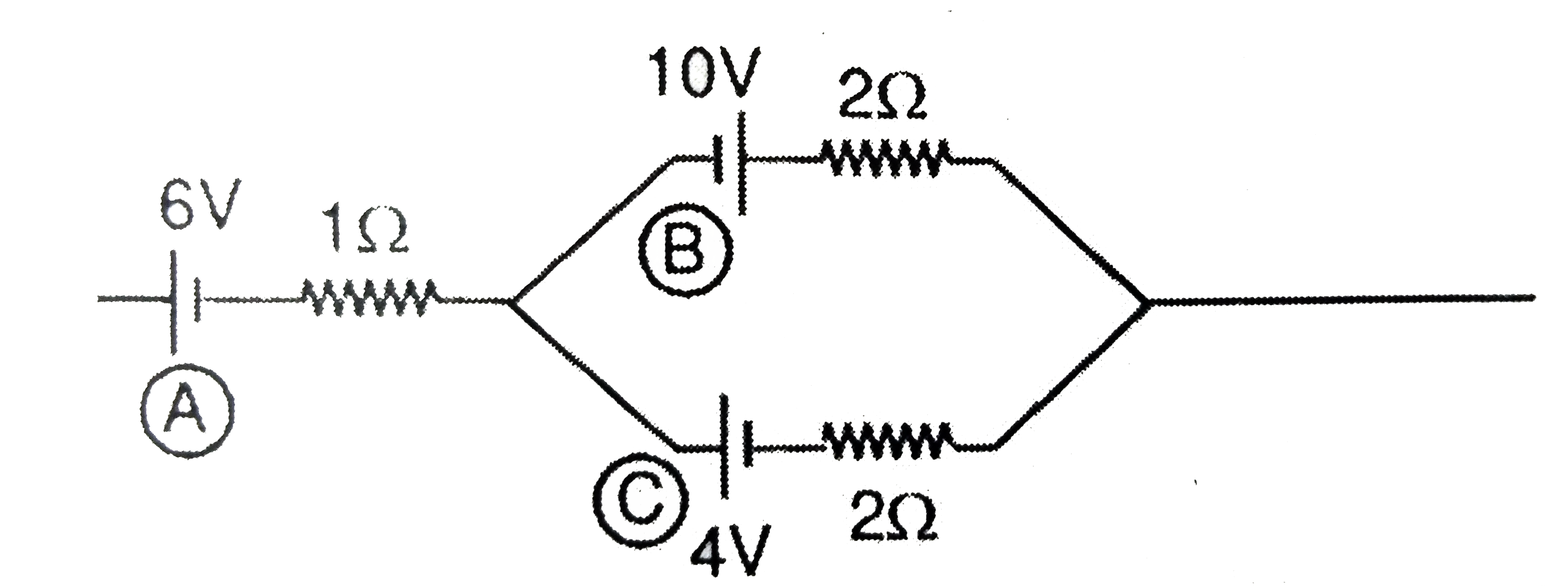
Battery (B) and ( C) are in parallel combination with opposite polarity. So, their equivalent
εBC=102+−4212+12=5−21=3V⇒rBC=1Ω.
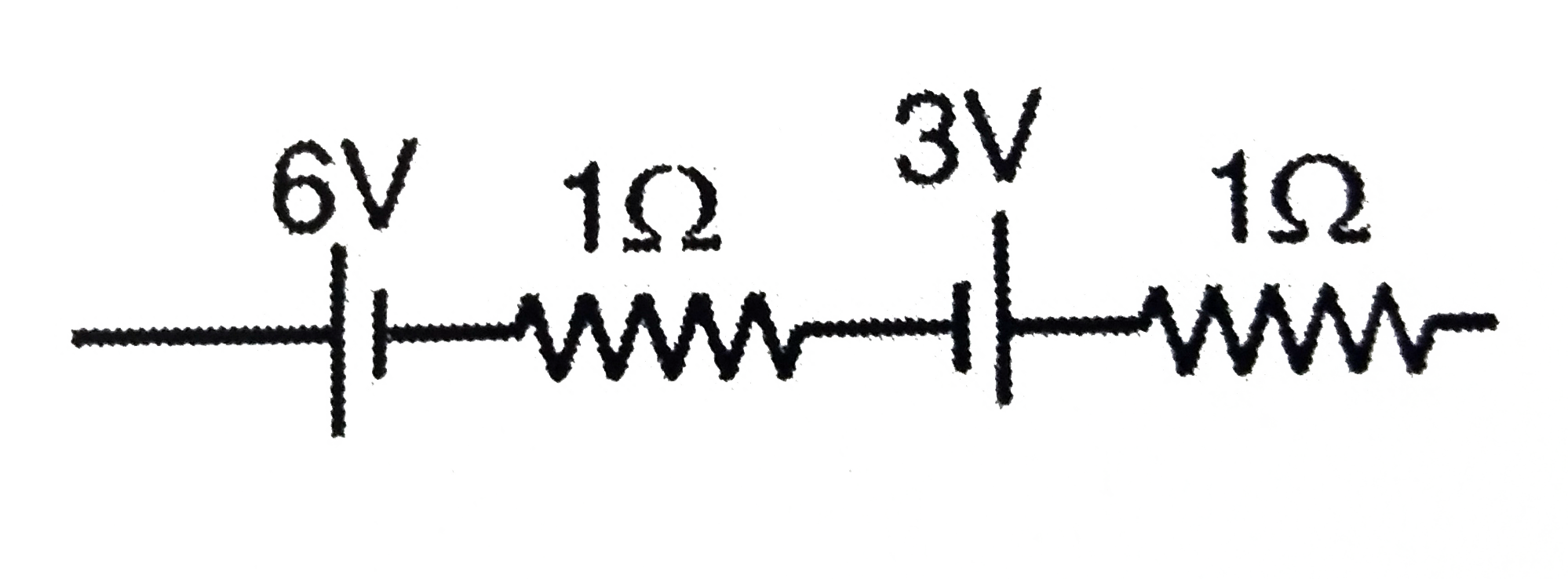
Now, εABC=6−3=3V
rABC=2Ω
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Solued miscellaneous Prolblems8videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)41videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
Similar Questions
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
 View Solution
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
 View Solution
View SolutionThe emf of the battery shown in figure is
 View Solution
View SolutionFind the net emf of the three batteries shown in figure
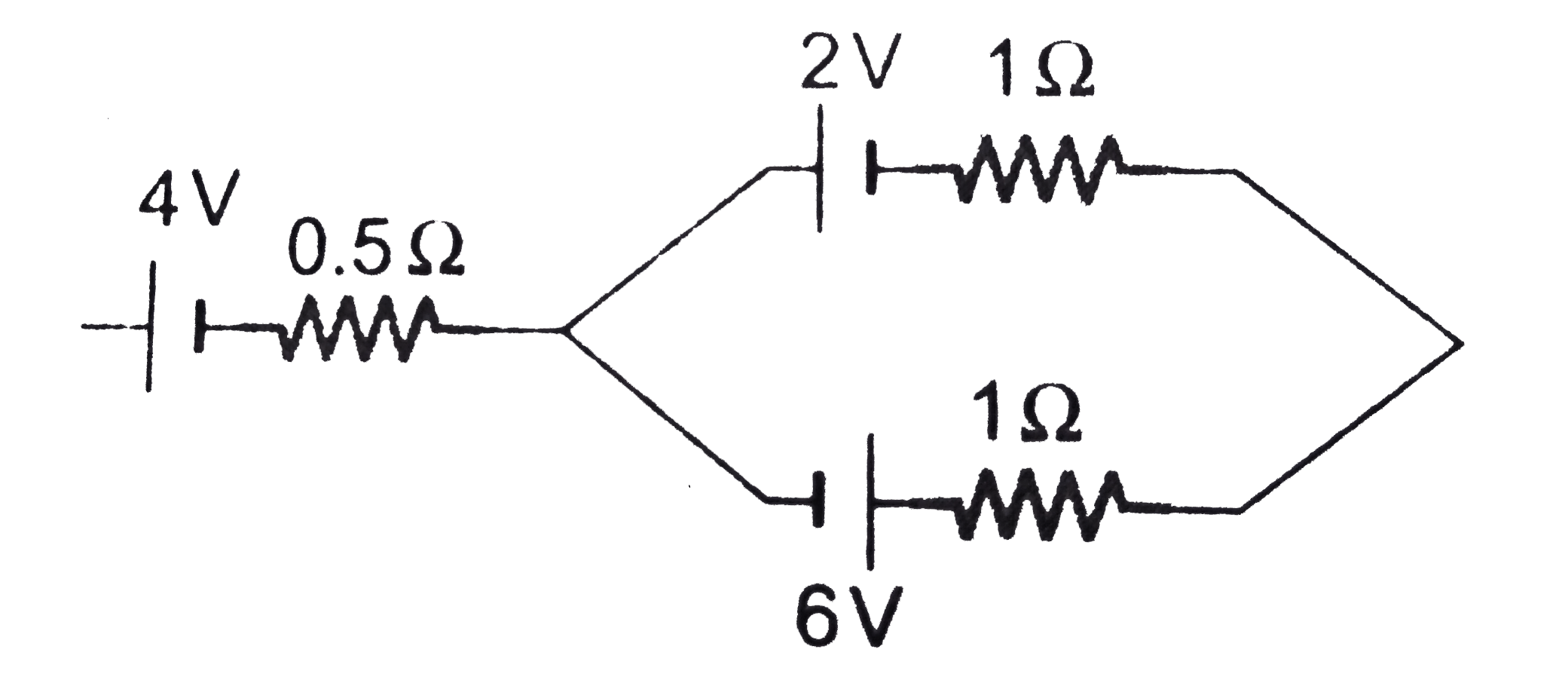 View Solution
View Solutionfind the emf of the battery shown in figure below:
 View Solution
View SolutionFind the equivalent emf and internal resistance of the arrangement shown in figure.
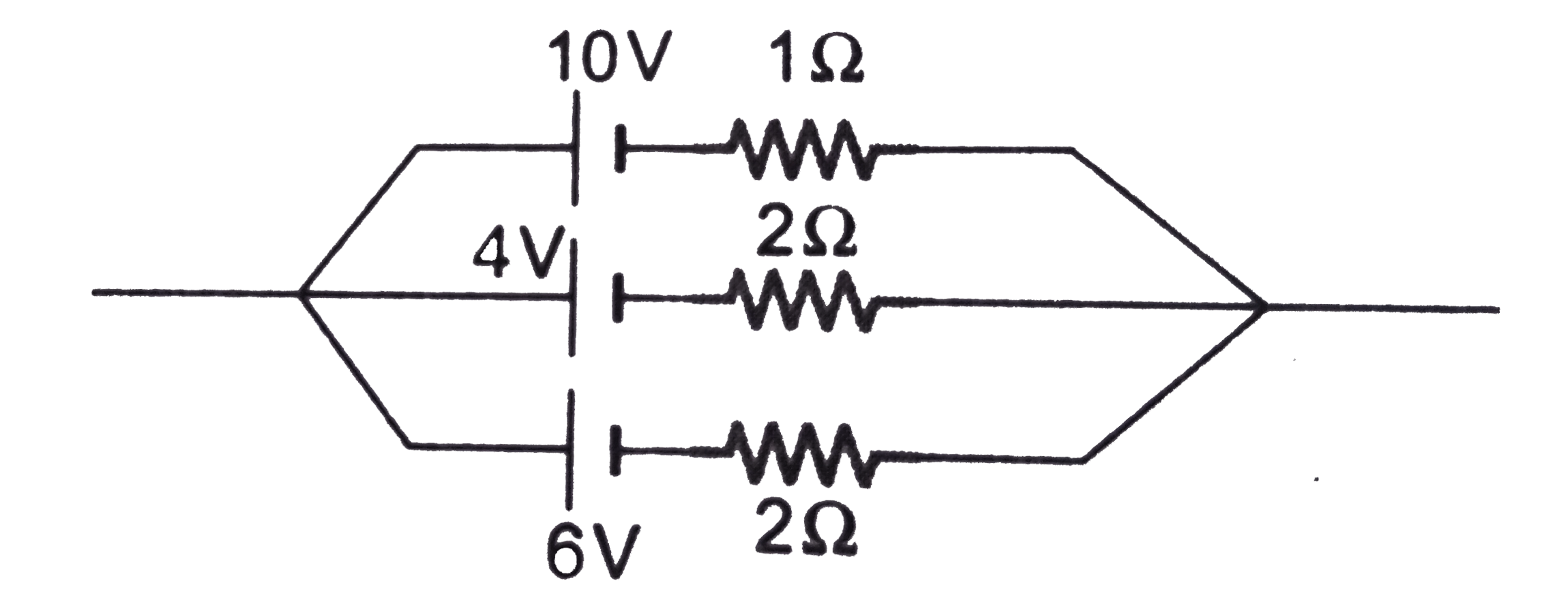 View Solution
View SolutionCalculate battery current and equivalent resistance of the network shown in figure.
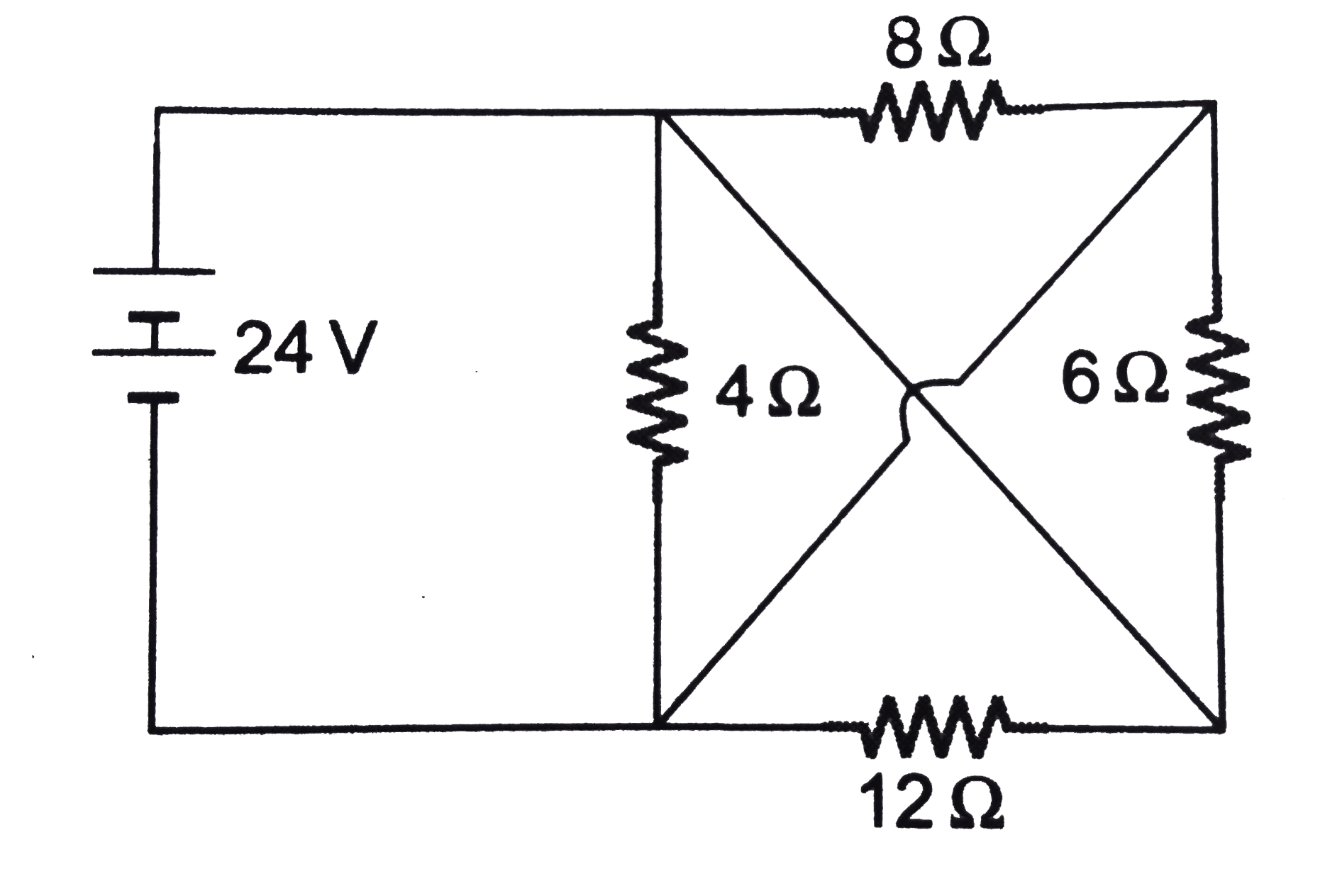 View Solution
View SolutionCalculate battery current and equivalent resistance of the network shown in figure.
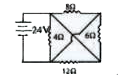 View Solution
View SolutionFor maximum power from battery the internal resistance of battery r is
 View Solution
View SolutionA single battery is connected to three resistances as shown in fig. 5.316
 View Solution
View Solution
