Find the current in each wire applying only Kirchhoff voltage law
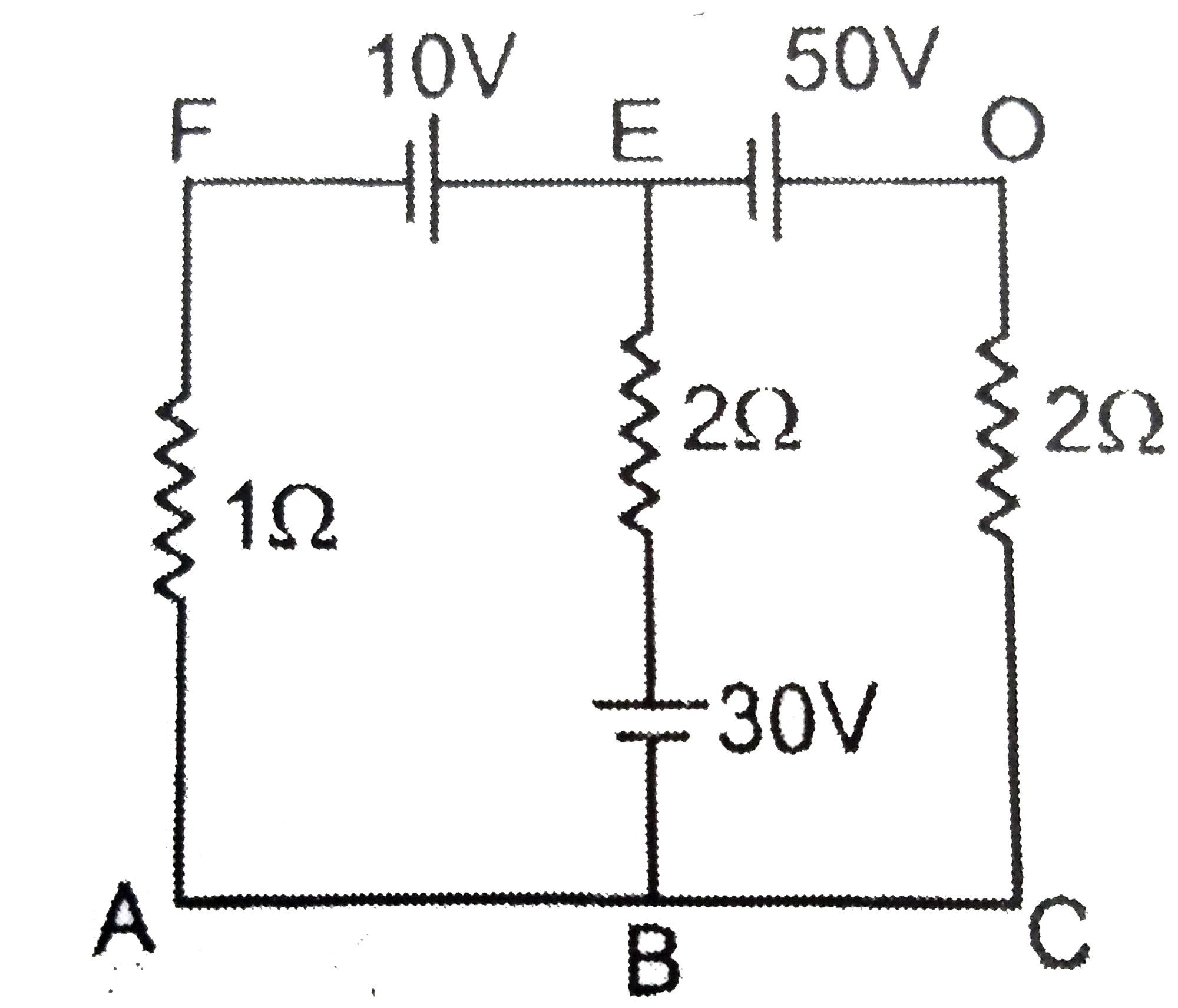
Applying Krichhoff voltage law in loop ABEF
i1+30+2(i1+i2)−10=0
3I1+2I2+20=0
Applying Kirchhoff voltage law in BEDCB
+30+2(i1+i2)+50+2i2=0
4i2+2i1+80=0
2i2+i1+40=0
Solving (i) and (ii)
3[−40−2i2]+2i2+20=0
−120−4i2+20=0
i2=−25 A and i1=10A ∴i1+i2=−15A
current in wire AF = 10 A form A to F
current in wire EB = 15 A from B to E
currnt in wire DE=25 A from E to D.

Topper's Solved these Questions
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Solued miscellaneous Prolblems
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-1)
Explore 41 Videos
- COMMUNICATION SYSTEMSBook:RESONANCE ENGLISHChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
Similar Questions
Find current in the wire BC.

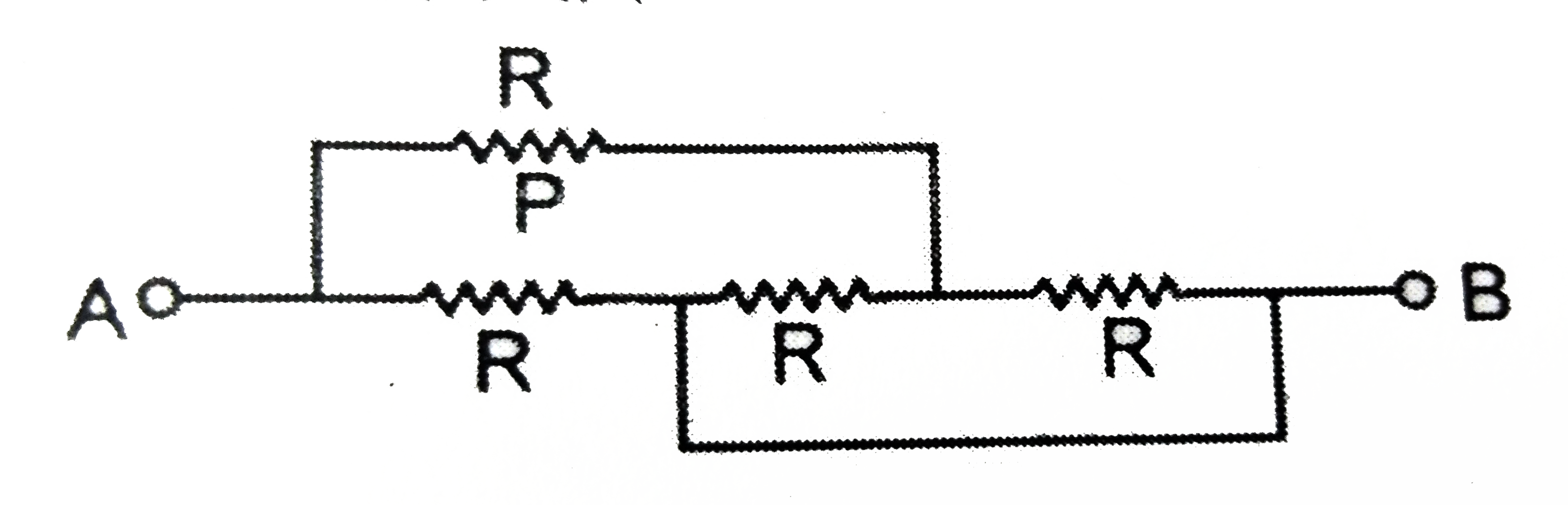
View SolutionFind the current in Resistance P if voltage supply between A and B is V volts.
View SolutionGiven below find the current in the wire BD.
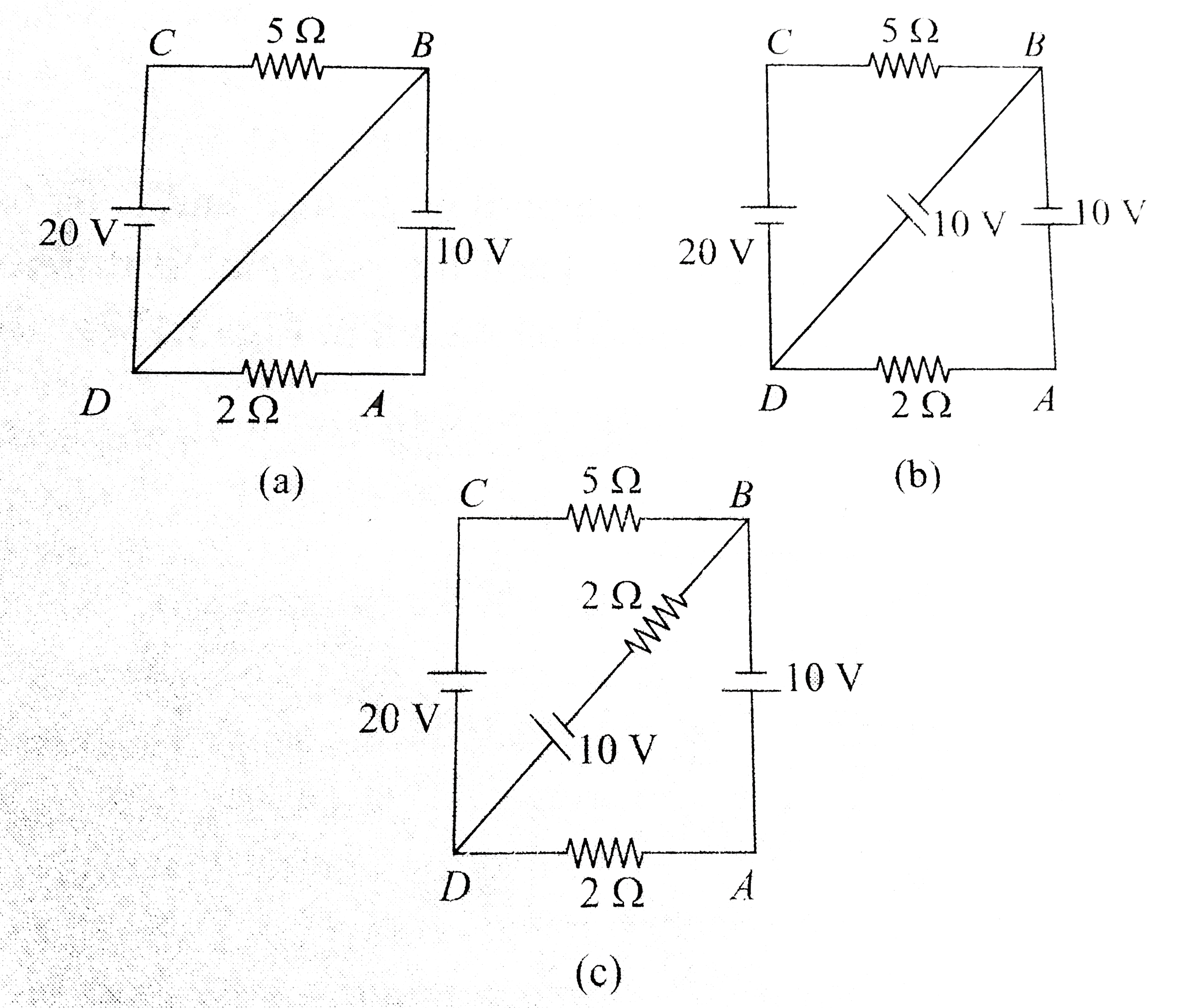
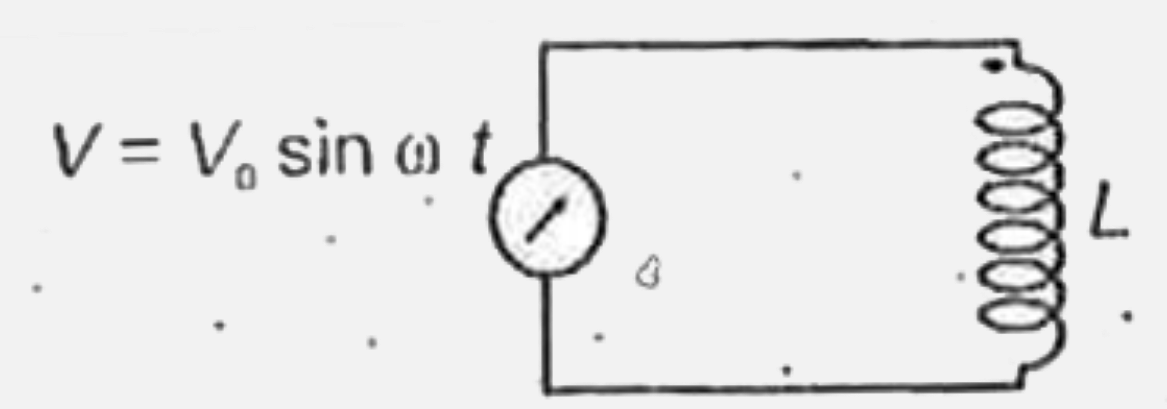
View SolutionThere is no resistance in the inductive circuit Kirchhoff 's voltage law for the circuit is
View SolutionFind the energy stored in the capacitor using Kirchhoff's Laws.
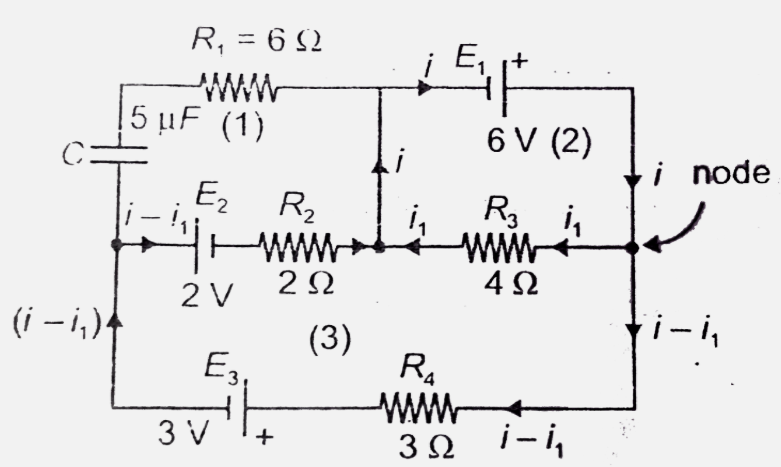
Strategy : Step-1 : Take the current from the batter of highest EMF
Step -2: Divide the total current into branch currents, keeping in mind that no current flows through capacitor.
Step-3 : Apply KVL to 3 loops shown in the figure.
Step -4 : Find the voltage across the capacitor using KVL
Step -5 : Apply the formula E=12CV2 to find energy
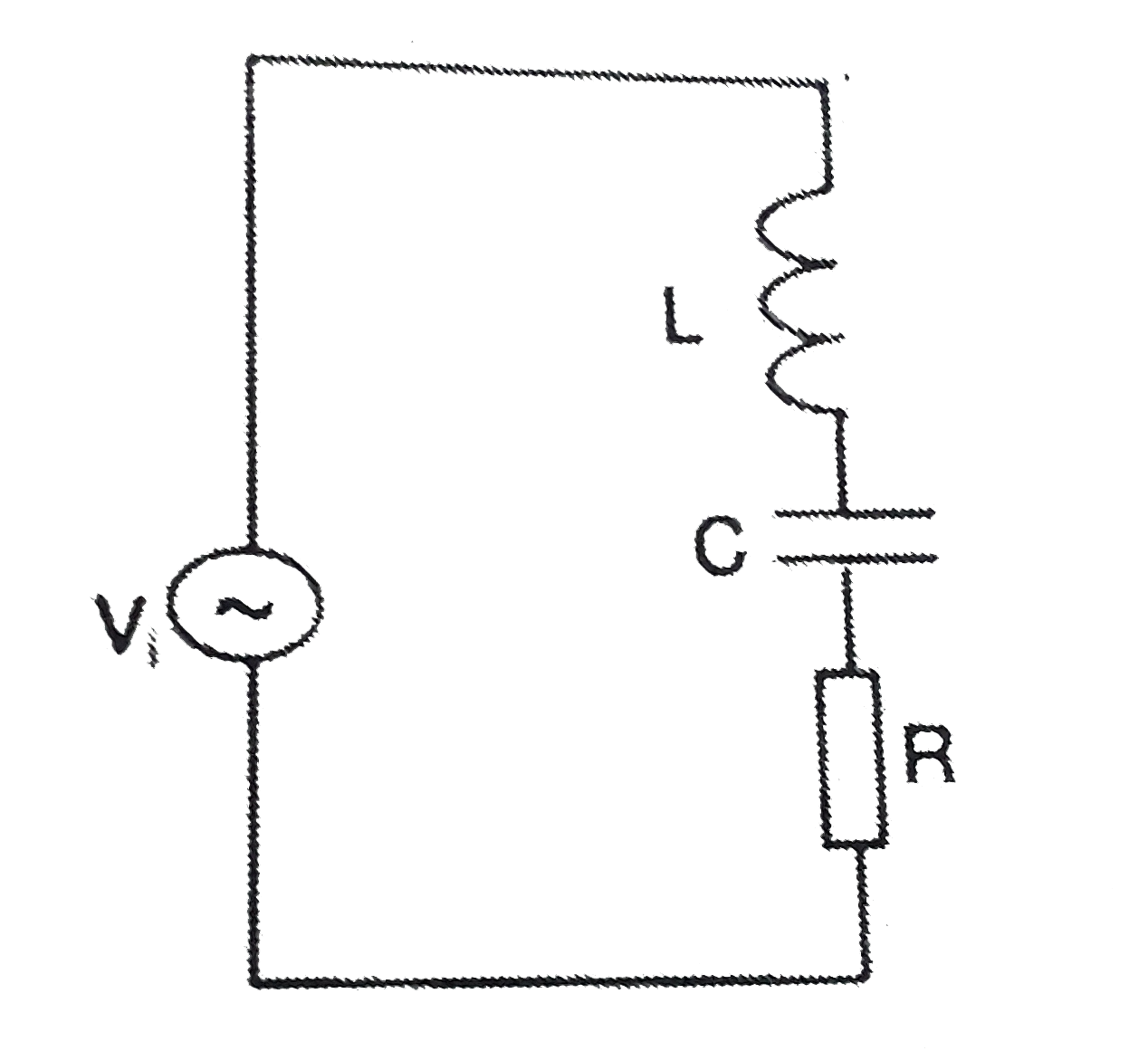
View SolutionIn the following circuit the current is in phase with the applied voltage. Therefore, the current in the circuit and the frequency of the source voltage respectively, are
View SolutionFind currents in different branches of th electric circuit shown in figure.
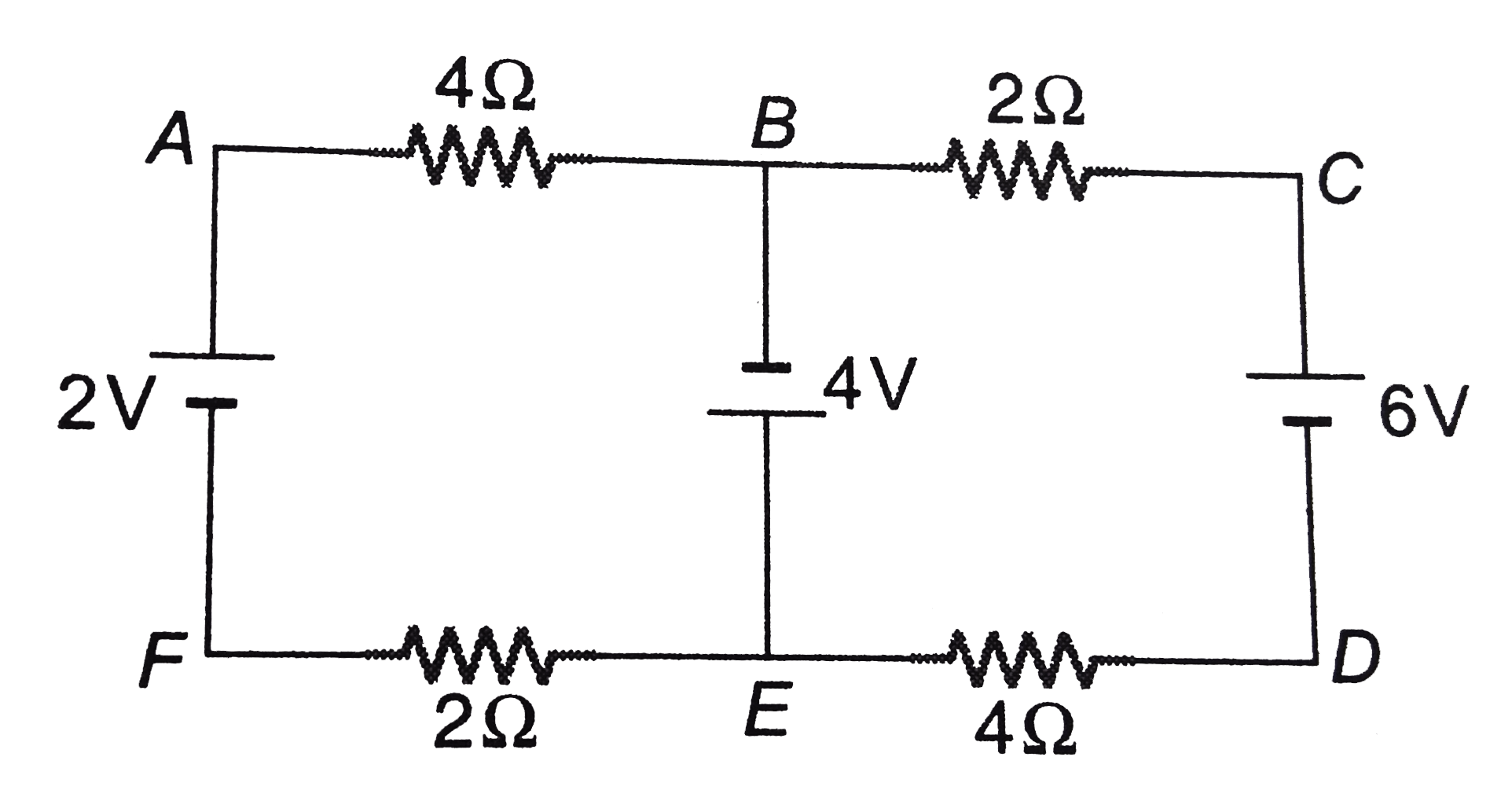 How to Proceed : In this problem there are three wires EFAB,BE and BCDE. Therefore, we have three unknown currents i1,i2 and i3. So, we require three equations. One equation will be obtained by applying Kirchhoff's junction law (either at B or at E) and the remainig two equations, we get from te second law (loop law). We can make three loops ABEFA,ACDF and BCDEB. But we have to chose any two of them. Initilly, we can choose any arbitrary directions of i1,i2 and i3.
How to Proceed : In this problem there are three wires EFAB,BE and BCDE. Therefore, we have three unknown currents i1,i2 and i3. So, we require three equations. One equation will be obtained by applying Kirchhoff's junction law (either at B or at E) and the remainig two equations, we get from te second law (loop law). We can make three loops ABEFA,ACDF and BCDEB. But we have to chose any two of them. Initilly, we can choose any arbitrary directions of i1,i2 and i3.
View SolutionIn the circuit shown in figure below, E1 and E2 are two cells having emfs 2 V and 3 V respectively, and negligible internal resistances. Applying Kirchhoff.s laws of electrical networks, find the values of currents I1 and I2.
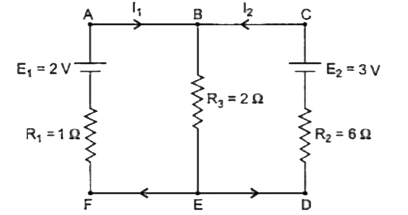
View SolutionIn the circuit shown in figure below, E1 and E2 are two cells having emf 2 V and 3 V respectively and negligible internal resistances. Applying Kirchhoff.s laws of electrical networks, find the values of currents I1 and I2.
View SolutionIn the circuit given, E1andE2 are two cells emfs 4 V and 6 V respectively, having negligible internal resistance. Applying Kirchhoff.s law of electrical networks, find the values of I1andI2.
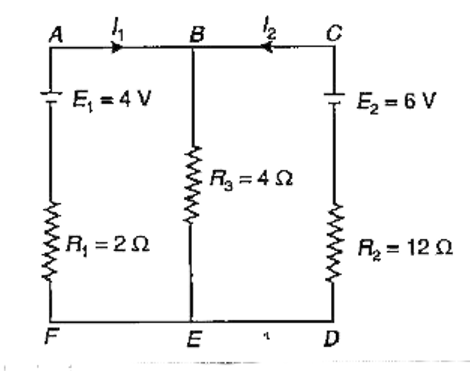
View Solution