At t=0, switch is closed, if initially C1 is uncharged and C2 is charged to a potential difference 2ε then find out following (Given C1=C2=C)
(a) Charge on C1 and C2 as a function of time.
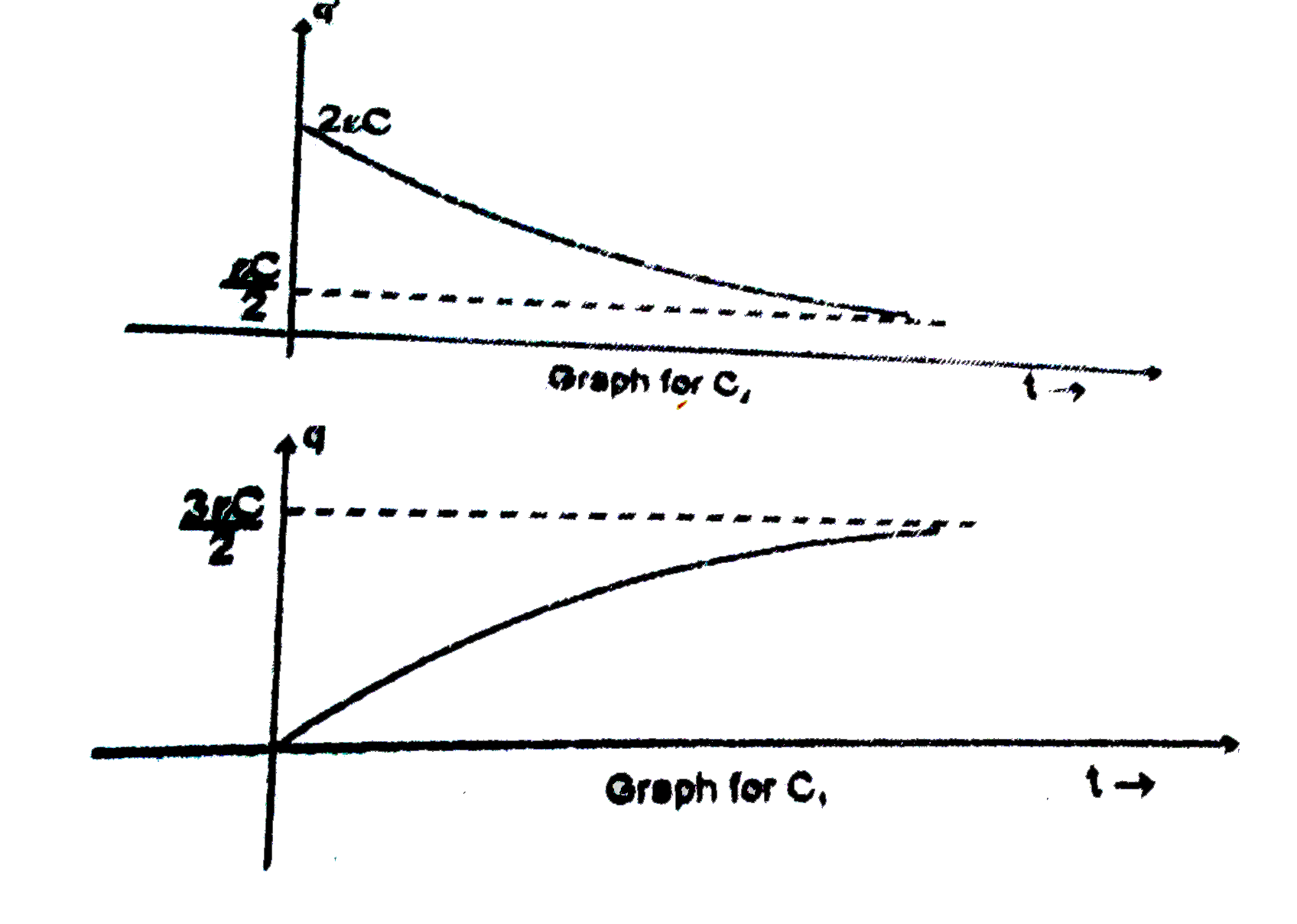
(b) Also plot the graphs for the relations derived in part (a).
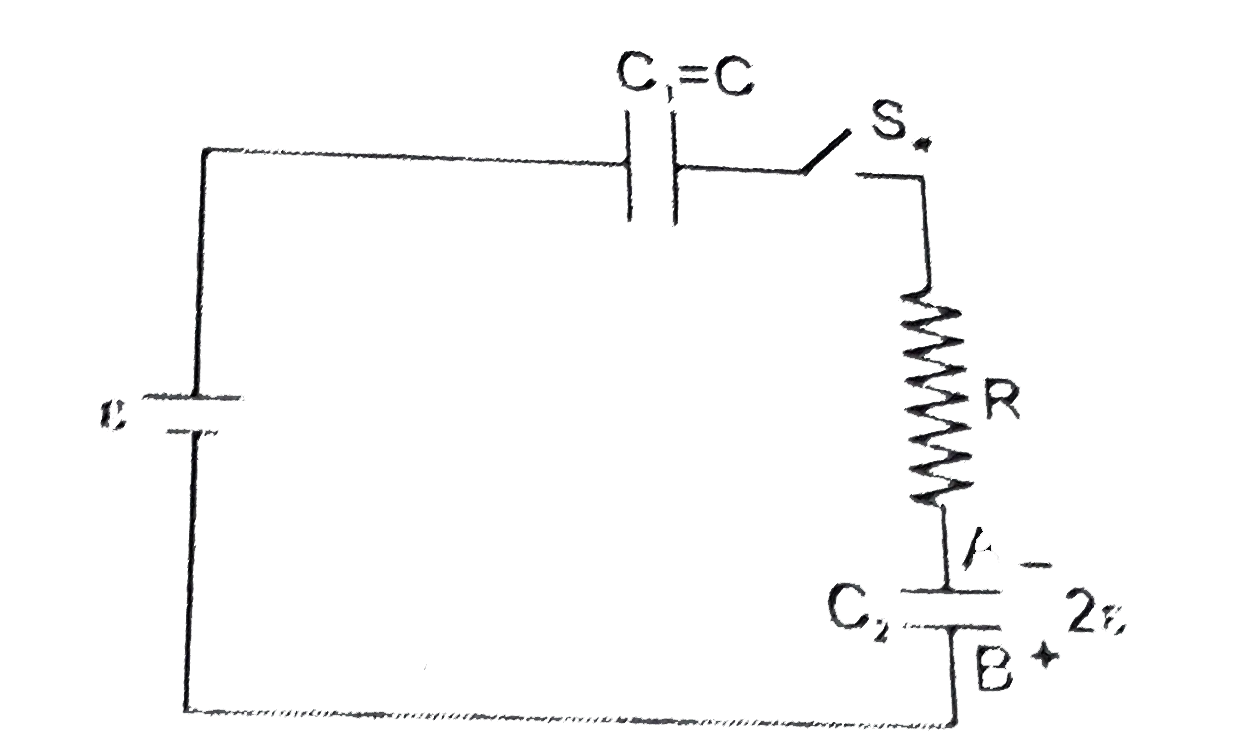
Let q charge flow in time 't' from the battery as shown. The charge on various plates of the capacitor is as shown in the figure. Now applying KVL
ε−qC−iR−q−2εCC=0
ε−qC−qC+2ε−iR=0
3ε=2qC+iR⇒3ε−iR=2qC
3εC−iRC=2q⇒dqdtRC=3εC−2q
∫q0dq3εC−2q=∫t0dtRC⇒−12ln(3Cε−2q3Cε)=tRC
In(3εC−2q3εC)=−2tRC⇒3εC−2q=3εC e−2t/RC
3εC(1−e−2t/RC)=2q⇒q=32εC(1−e−2t/RC)
(charge on C, as function of time)
i=dqdt=3εRe−2t/RC
Charge on C2 as function of time :
q'=2εC−q
=2εC−32εC+32εCe−2t/RC
=εC2+32εCe−2t/RC
=εC2[1+3e−2t/RC]
Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example
3 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 1
79 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
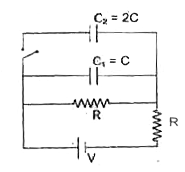
When switch is closed , charges on C1andC2 are
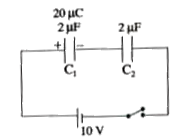
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged

Potential difference on C1just after closing the switch is
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionIn the circuit shown initially C1,C2 are uncharged. After closing the switch
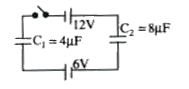
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
Charge on C2 just after closing the switch is
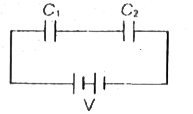
View SolutionTwo capacitors C1 and C2 are charged to same potential V, but with opposite polarity as shown in the figure. The switches S1 and S2 are then closed

View SolutionIn the circuit below, if dielectric is inserted inot C2 then the charge on C1 will
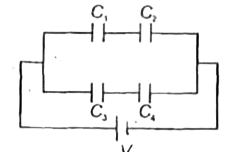
View SolutionFind the charge on capacitor C3
Given, then C1=C2andC3=C4 = 3 C .
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionIn the circuit shown, C1=C2=2μF. Capacitor C1 is charged to 50V and C1 is charge to 20V. After charging they are connected as shown. When S1,S2, and S3, are clsosed,
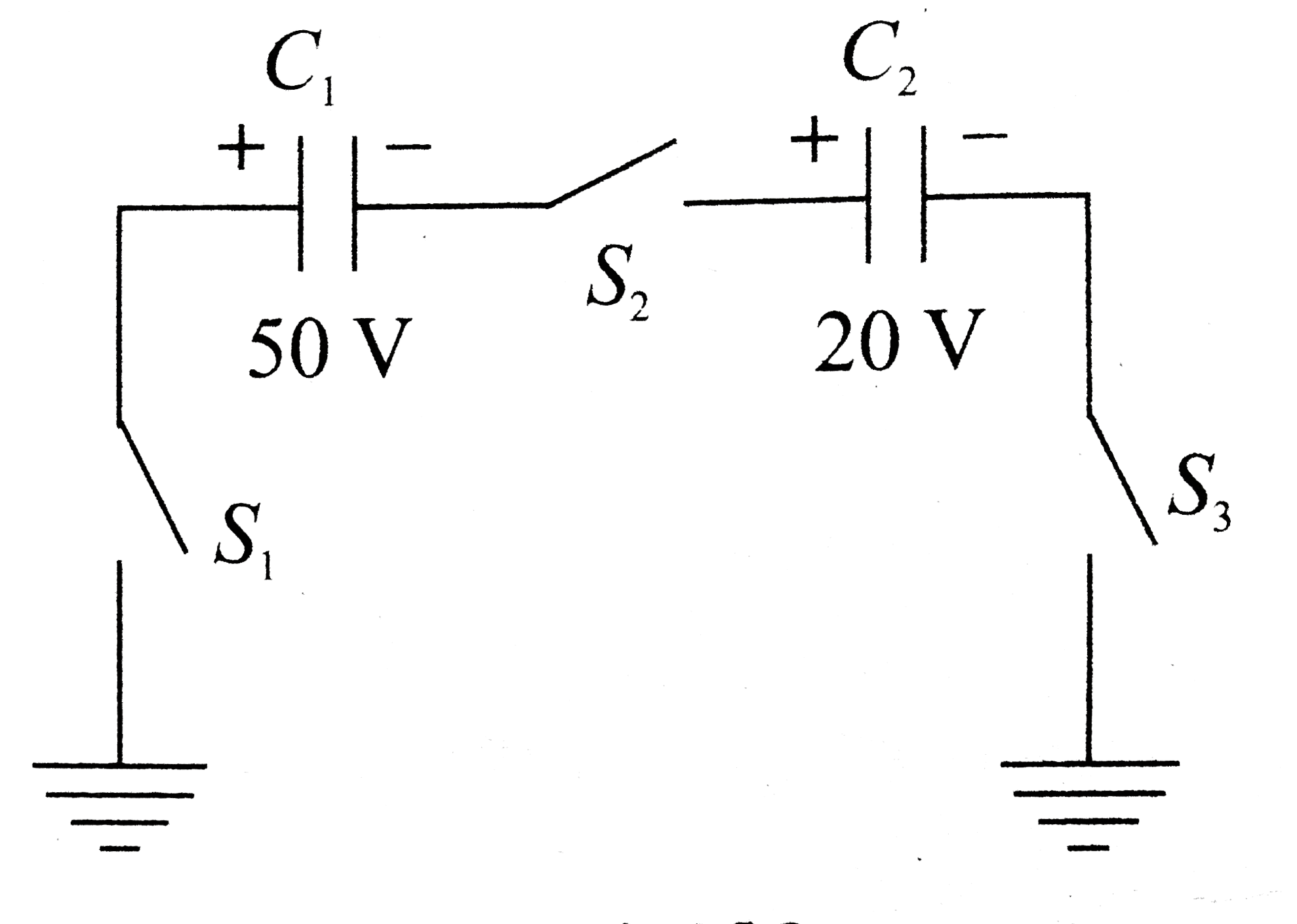 .
.
View Solution
