A curve y=f(x) passes through the origin. Through any point (x,y) on the curve, lines are drawn parallel to the co-ordinate axes. If the curve divides the area formed by these lines and co-ordinates axes in the ratio m:n, find the curve.
Area (OAPB)=xy⇒Area(OAPO)=x∫0f(t)dt
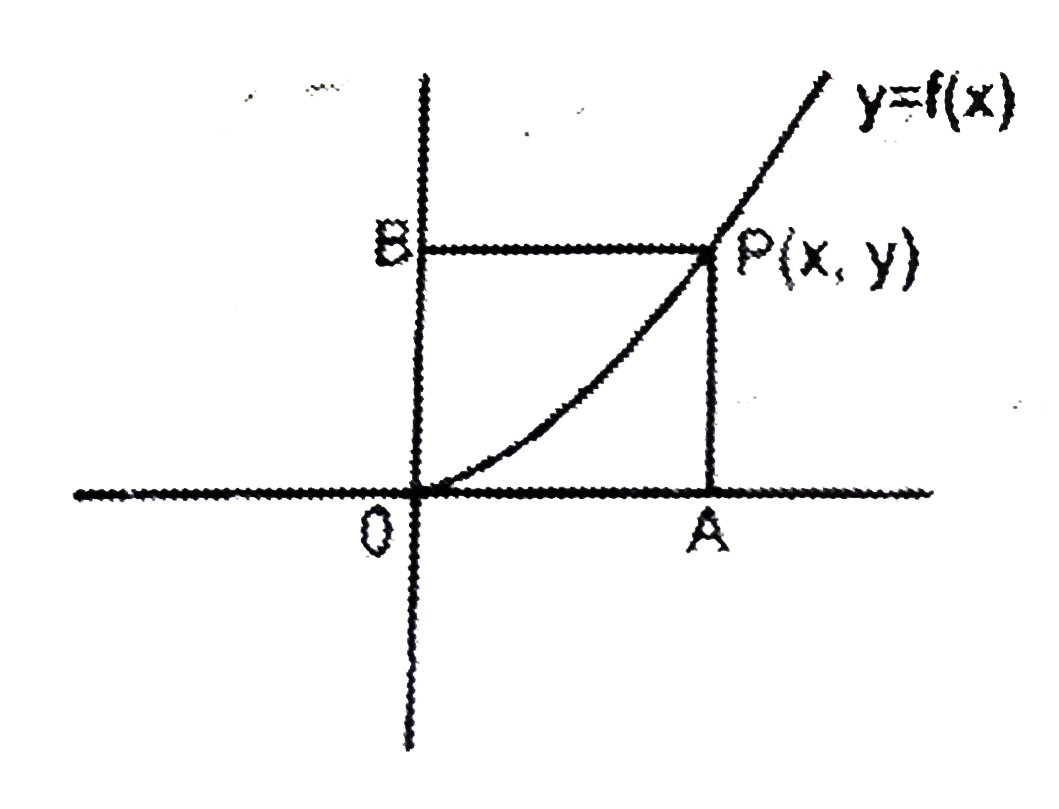
Area (OPBO)=xy−x∫0f(t)dt⇒Area(OAPO)Area(OPBO)=mn
nx∫0f(t)dt=m⎛⎜⎝xy−x∫0f(t)dt⎞⎟⎠⇒nx∫0f(t)dt=mxf(x)−mx∫0f(t)dt
Differentiating w.r.t x
nf(x)=mf(x)+mxfcancelc(x)-mf(x) rArr (f'(x))/(f(x)) = n/m = 1/x
f(x)=cxn/m
similarly f(x)=cxm/n
Topper's Solved these Questions
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCE ENGLISHCHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Self practive problem
106 Videos
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCE ENGLISHCHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - Exercise 1
64 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
- DPPBOOK - RESONANCE ENGLISHCHAPTER - DPPEXERCISE - QUESTION
656 Videos
Similar Questions
A curve y=f(x) passes through the origin. Through any point (x,y) on the curve, lines are drawn parallel to the coordinate axes. If the curve divides the area formed by these lines and coordinates axes in the ratio m:n , find the curve.
View SolutionThrough any point (x,y) of a curve which passes through the origin, lines are drawn parallel to the coordinate axes. Given that it divides the rectangle formed by the two lines and the axes into two areas one of which is twice the other, show that such a curve is parabola.
View SolutionFind the equation of lines drawn parallel to co-ordinate axes and passing through the point (−1,4).
View SolutionThe finite area of the region formed by co-ordinate axes and the curve y=logex is
View SolutionFind the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axes.
View SolutionIf the tangent line at a point (x, y) on the curve y=f(x) is parallel to y-axis, find the value of dxdy .
View SolutionFind the eqn of lines which pass through the point (1, 2) and equally inclined to the co- ordinate axes.
View SolutionA curve passes through the point (5,3) and at any point (x,y) on it, the product of its slope and the ordinate is equal to its abscissa. Find the equation of the curve and identify it.
View SolutionThe curve y=ax2+bx+c passes through the point (1,2) and its tangent at origin is the line y=x. The area bounded by the curve, the ordinate of the curve at minima and the tangent line is
View SolutionThe point on the curve xy2=1 nearest to origin is_________. {Determine the co-ordinates of the point.}
View Solution
