Question

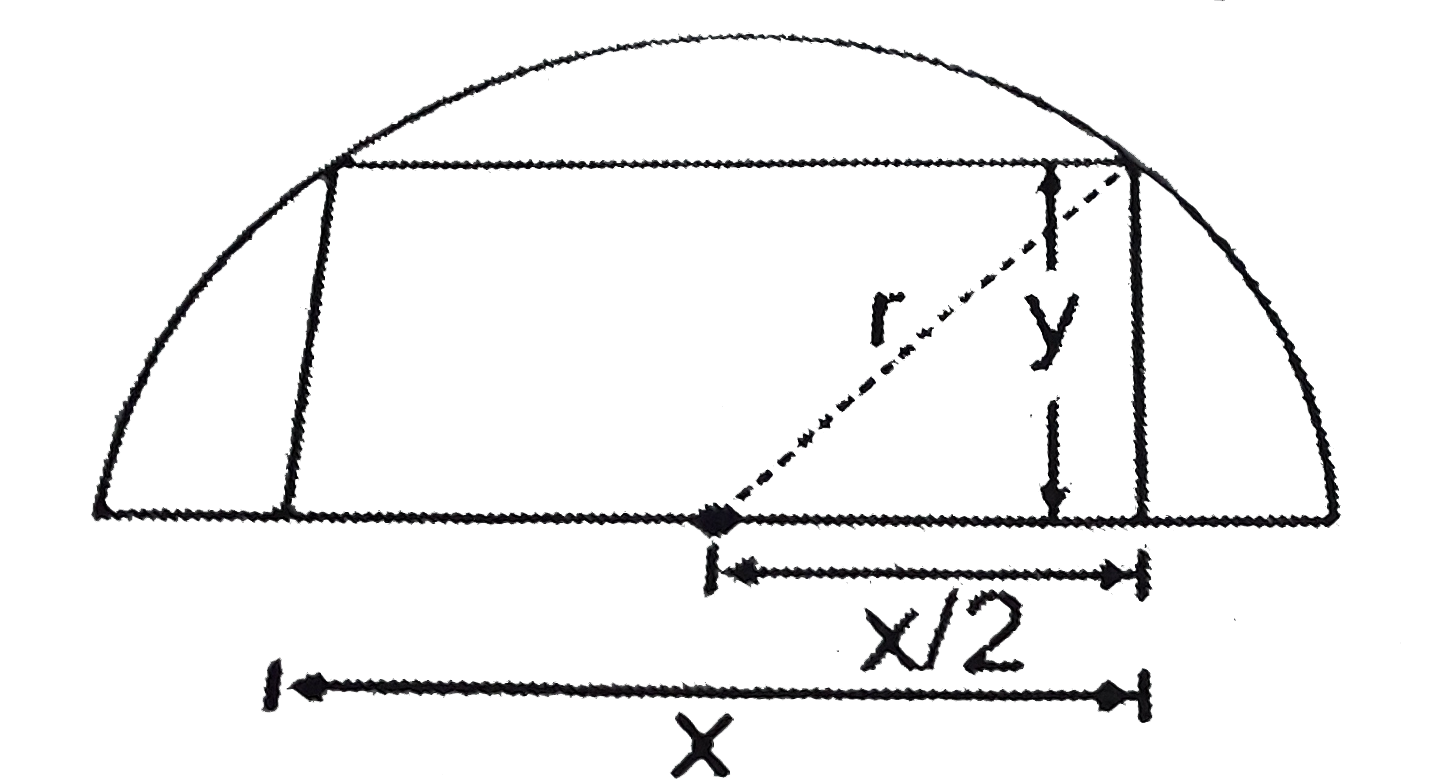
Rectangles are inscribed inside a semi-circle of radius $r\stackrel{.}{}$
Find the rectangle with maximum area.

Explanation

Let sides of rectangle be x and y (as show in figure).
`rArr " " A=xy`
Hence x and y are not independent variables and are related by Pythogorus theorem with r.
`(x^(2))/(4)+y^(2) =r^(2) " rArr " "y=sqrt(r ^(2)-(x^(2))/(4))`
`rArr " " A(x) =x sqrt(x^(2) -(x^(2))/(4))`
`rArr " "A(x) =sqrt(x^(2)r^(2) -(x^(4))/(4))`
`"Let "" "f(x) =r^(2)x^(2) -(x^(4))/(4), " "x in (0,r)`

A(x) is maximum when f(x) is maximum
Hence `f(x) =x(2r^(2)-x^(2)) =0" "rArr " "x = r sqrt(2)`
`"also"" " f(rsqrt(2)) lt 0 " and " f(rsqrt(2)) gt0`
confirming at f(x) is maximum when x =r `sqrt(2) & y =(r)/(sqrt(2))`.