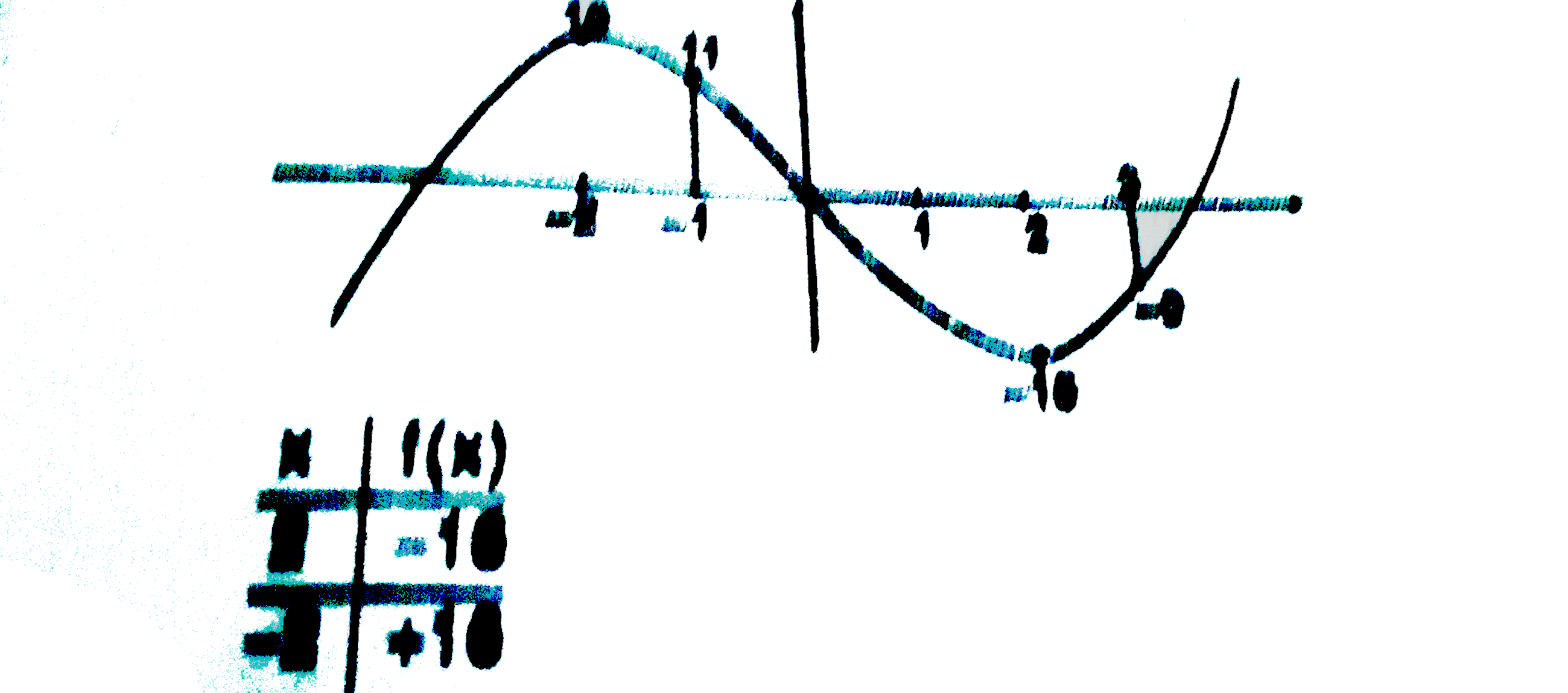
Find the points of maxima minima of f(x) =x3−12x. Also draw the graph of this functions.
f(x)=x3−12x
f'(x)=3(x2−4)=3(x−2)(x+2)
⇒ x=±2

for tracing the graph let us find maximum and minimum values of (x) .
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:RESONANCE ENGLISHChapter:APPLICATION OF DERIVATIVESExercise:Self Practice Problems
Explore 36 Videos
- APPLICATION OF DERIVATIVESBook:RESONANCE ENGLISHChapter:APPLICATION OF DERIVATIVESExercise:Exersise -1A
Explore 5 Videos
- COMBINATORICSBook:RESONANCE ENGLISHChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 5 Videos
Similar Questions
Find the points of maxima or minima of f(x) =x2(x−2)2.
View SolutionFind points of local maxima /minima of
f(x)=x2e−x.
View SolutionDraw the graph of the function f(x)=xx
View SolutionDraw the graph of the function f(x)=|x−1|
View SolutionFind the possible points of Maxima/Minima for f(x)=∣∣x2−2x∣∣(X∈R)
View SolutionDraw the graph of the function f(x)=−x|x|.
View SolutionFind the points of local maxima and minima of the function f(x)=x2−4x.
View SolutionFind the points of local maxima or minima for f(x)= sin 2x−x,x∈(0,π)
View SolutionDraw the graph of the function: f(x)=log|x|
View SolutionLet f(x) =x3−x2−x−4
(i) find the possible points of maxima /minima of f(x) x∈R
(ii) Find the number of critical points of f(x) x∈[1,3]
(iii) Discuss absolute (global) maxima / minima value of f(x) for x∈[−2,2]
(iv) Prove that for x∈(1,3) the function does not has a Global maximum.
View Solution