If area of circle increases at a rate of 2cm2/sec then find the rate at which area of the inscribed square increases.
To solve the problem, we need to find the rate at which the area of the inscribed square increases when the area of the circle increases at a rate of 2cm2/sec.
1. Understanding the relationship between the circle and the inscribed square:
- Let the radius of the circle be r.
- The area A of the circle is given by the formula:
A=πr2
2. Differentiating the area of the circle with respect to time:
- We know that the area of the circle is increasing at a rate of dAdt=2cm2/sec.
- Differentiating the area of the circle with respect to time t:
dAdt=2πrdrdt
- Setting this equal to the given rate of increase:
2πrdrdt=2
- Simplifying gives:
πrdrdt=1(Equation 1)
3. Finding the relationship between the radius of the circle and the side of the inscribed square:
- The side length d of the inscribed square can be expressed in terms of the radius r of the circle:
d=r√2
- Therefore, the area As of the square is:
As=d2=(r√2)2=2r2
4. Differentiating the area of the square with respect to time:
- Differentiating the area of the square:
dAsdt=4rdrdt
5. Substituting from Equation 1:
- From Equation 1, we have πrdrdt=1, which gives:
drdt=1πr
- Substituting this into the differentiation of the area of the square:
dAsdt=4r(1πr)=4π
6. Final Result:
- Thus, the rate at which the area of the inscribed square increases is:
dAsdt=4πcm2/sec
Summary:
The rate at which the area of the inscribed square increases is 4πcm2/sec.
- Let the radius of the circle be r.
- The area A of the circle is given by the formula:
A=πr2
- We know that the area of the circle is increasing at a rate of dAdt=2cm2/sec.
- Differentiating the area of the circle with respect to time t:
dAdt=2πrdrdt
- Setting this equal to the given rate of increase:
2πrdrdt=2
- Simplifying gives:
πrdrdt=1(Equation 1)
- The side length d of the inscribed square can be expressed in terms of the radius r of the circle:
d=r√2
- Therefore, the area As of the square is:
As=d2=(r√2)2=2r2
- Differentiating the area of the square:
dAsdt=4rdrdt
- From Equation 1, we have πrdrdt=1, which gives:
drdt=1πr
- Substituting this into the differentiation of the area of the square:
dAsdt=4r(1πr)=4π
- Thus, the rate at which the area of the inscribed square increases is:
dAsdt=4πcm2/sec
The rate at which the area of the inscribed square increases is 4πcm2/sec.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
36 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
Similar Questions
The radius of a circle is increasing uniformly at the rate of 4 cm/sec. Find the rate at which the area of the circle is increasing when the radius is 8 cm.
View SolutionThe radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
View SolutionRadius of a circle is increasing at rate of 3cm/sec Find the rate at which the area of circle is increasing at the instant when radius is 10 cm.
View SolutionAn equilateral triangle's sides increase at the rate of 2cm/sec. If the area of its incircle increases at a rate of kcm2/sec (when the length of the side is 6πcm), then the value of k is
View Solution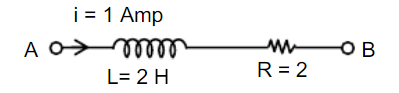
If current is increases with rate of 2Ampsec, then find VA−VB
View SolutionIf the radius of a circle is increasing at a uniform rate of 2 cm/s, then find the rate of increase of area of circt the instant when the radius is 20 cm.
View SolutionA stone is dropped in a quiet lake. If the produced circular waves increase at a rate of 4 cm/sec, then find the rate of increase in its area when the redius of circular wave is 7 cm.
View SolutionThe volume of a spherical balloon is increasing at a rate of 25cm3/sec. Find the rate of increase of its curved surface when the radius of balloon is 5 cm.
View SolutionThe sides of an equilateral triangle are increasing at the rate of 2 cm/sec. Find the rate at which the area increases, when the side is 10 cm.
View SolutionThe volume of cube is increasing at a rate of 9cm3/sec. Find the rate of increase of its surface area when the side of the cube is 10 cm.
View Solution
