Find the equation of all straight lines which are tangent to curve y=1x−1 and which are parallel to the line x+y =0.
Suppose the tangent is at (x,.Y,) and it has slope -1
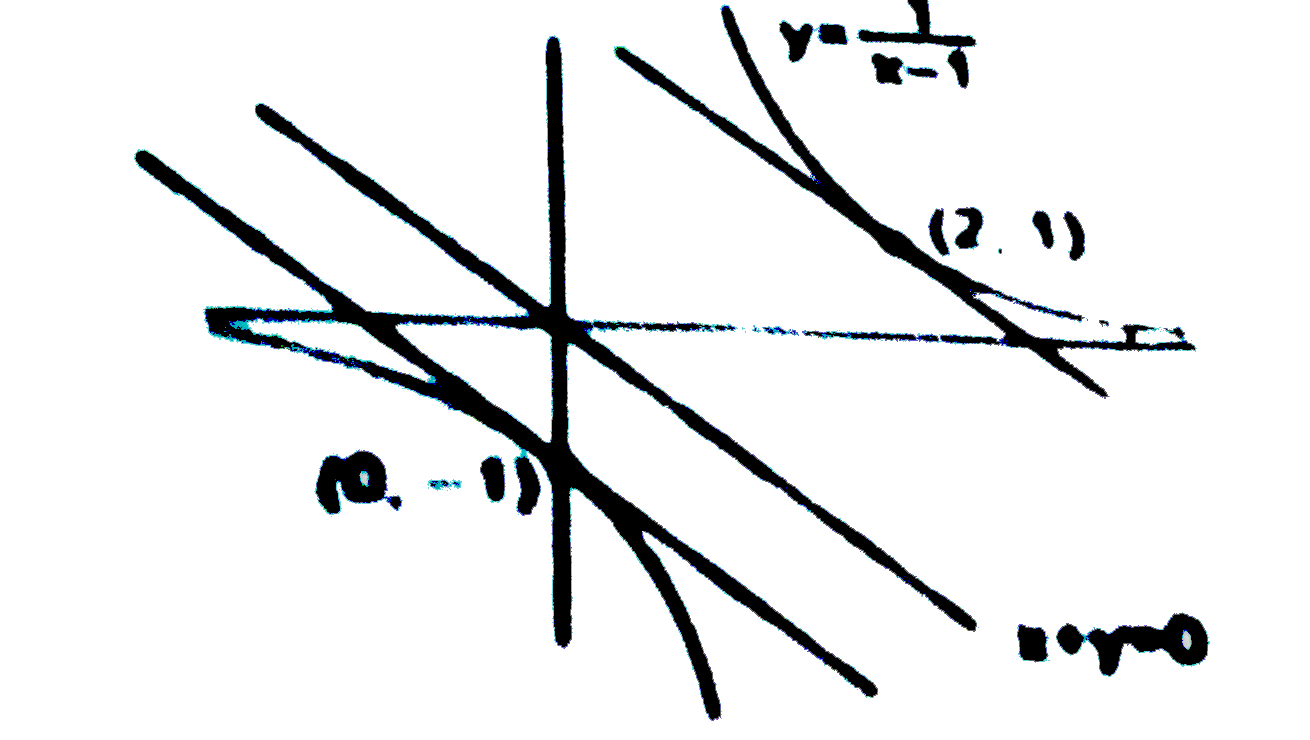
⇒ dydx∣x1y=−1
⇒ −1(x1−1)2=−1
⇒ x1=0 or 2
⇒ y1=1 or 1
Hence tangent at (0,−1) and (2,1) and the required lines (see figure ) with equations
−1(X−0)=(y+1) and −1(x−2)=(y−1)
⇒ X+y+1=0 and y+x=3
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:RESONANCE ENGLISHChapter:APPLICATION OF DERIVATIVESExercise:Self Practice Problems
Explore 36 Videos
- APPLICATION OF DERIVATIVESBook:RESONANCE ENGLISHChapter:APPLICATION OF DERIVATIVESExercise:Exersise -1A
Explore 5 Videos
- COMBINATORICSBook:RESONANCE ENGLISHChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 5 Videos
Similar Questions
Find the equations of all lines having slope 0 which are tangent to the curve y=1x2−2x+3.
View SolutionFind the equation of all lines having slope −1that are tangents to the curve y=1x−1,x≠1.
View SolutionFind the equation of all lines having slope 2 and being tangent to the curve y+2x−3=0.
View SolutionFind the equation of the tangent to the curve y=√3x−2 which is parallel to the line 4x−2y+5=0.
View SolutionFind the equation of the straight line which is such that
it passes through the point (4, 3) and is parallel to the line 3x−4y+5=0.
View SolutionFind the equation of the tangent to the curve y=√3x−2 which is parallel to the line 4x−2y+5=0.
View SolutionFind the equation of the tangent line to the curve y=x2−2x+7which is(a) parallel to the line 2xy+9=0(b) perpendicular to the line 5y15x=13.
View SolutionFind the equation of the tangent to the curve y=√4x−2 which is parallel to the line 4x−2y+5=0
View SolutionFind the equations of all lines of slope zero and that are tangent to the curve y=1x2−2x+3 .
View SolutionFind the equations of all lines having slope 2 and that are tangent to the curve y=1x−3, x≠3 .
View Solution

