Find equation of tangent to y =ex at x=0 . Hence draw graph
Atx=0 ⇒ y=e0=1
dydx = ex ⇒ dydx∣x=0=1
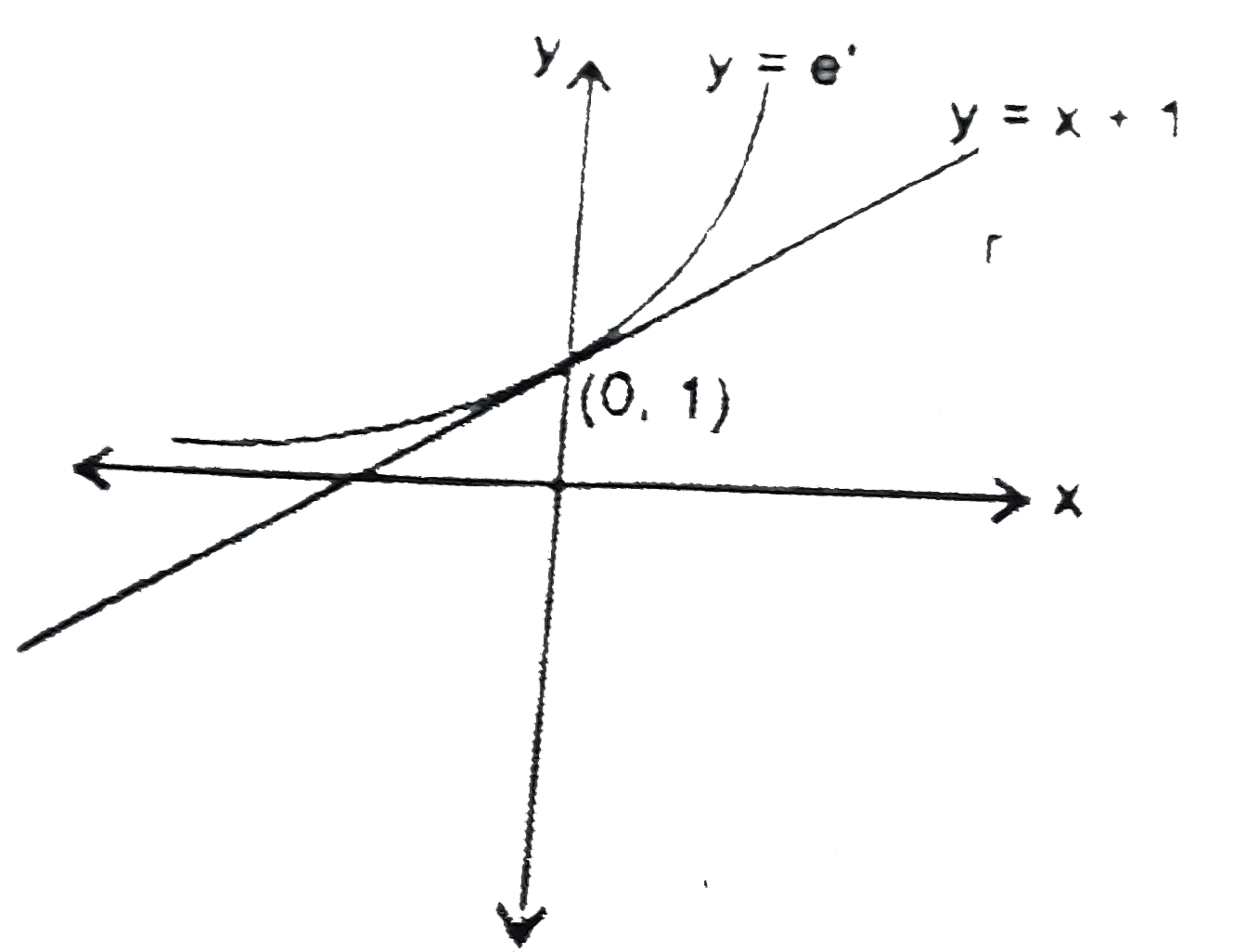
Hence equation of tangent is
1(x−0)=(y−1)
⇒ y=x+1
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
36 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
Similar Questions
Knowledge Check
The equation of the tangent to the curve y=e2x at (0,1) is
AA) y + 1 = 2 xBB) 1 - y = 2 xCC) y - 1 = 2 xDD) none of these
Find the equation of tangents to hyperbola x2−y2−4x−2y=0 having slope 2.
View SolutionFind the equation of tangent to the hyperbola y=x+9x+5 which passes through (0,0) origin
View SolutionTo find the point of contact P(x1,y1) of a tangent to the graph of y=f(x) passing through origin O, we equate the slope of tangent to y=f(x) at P to the slope of OP. Hence we solve the equation f'(x)=f(x1)x1 to get x1 and y1.Now answer the following questions (7 -9): The equation |lnmx|=px where m is a positive constant has a single root for
View SolutionFind the equation of tangent of tangent of the curve y = b⋅e−x/a at that point at which the curve meets the Y-axis.
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1)
View SolutionFind the equation of tangent to the conic x2−y2−8x+2y+11=0 at (2,1).
View SolutionFind the equation of the tangent to the circle x2+y2−2x−2y−23=0 and parallel to 2x+y+3=0.
View Solution
