C(s)⇔2A(g)+B(s)
If the dissociation of C(s) is α and d is the density of the gaseous mixture in the container. Initially container have only C(s) and the reaction is carried at constant temperature and pressure.
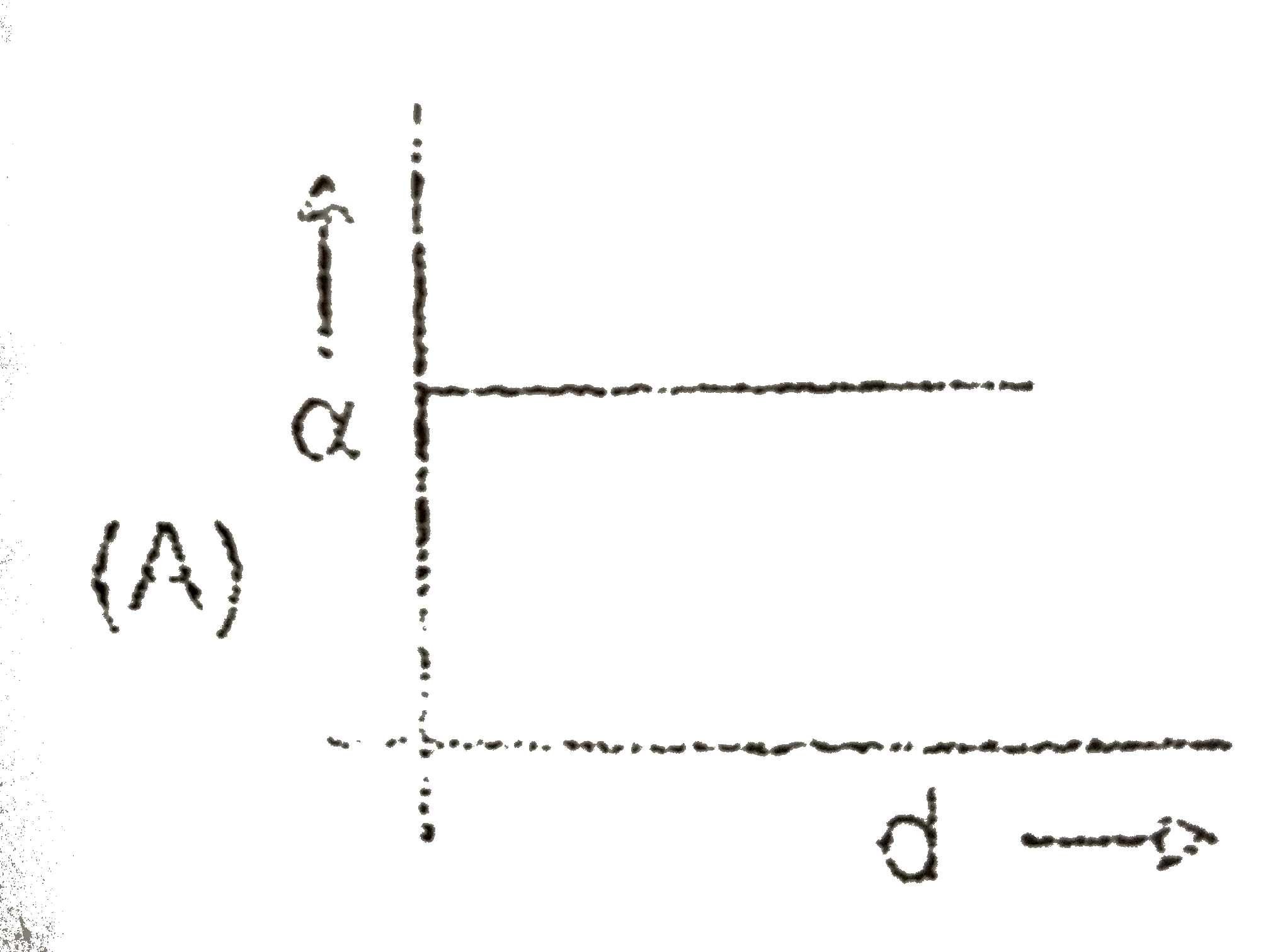
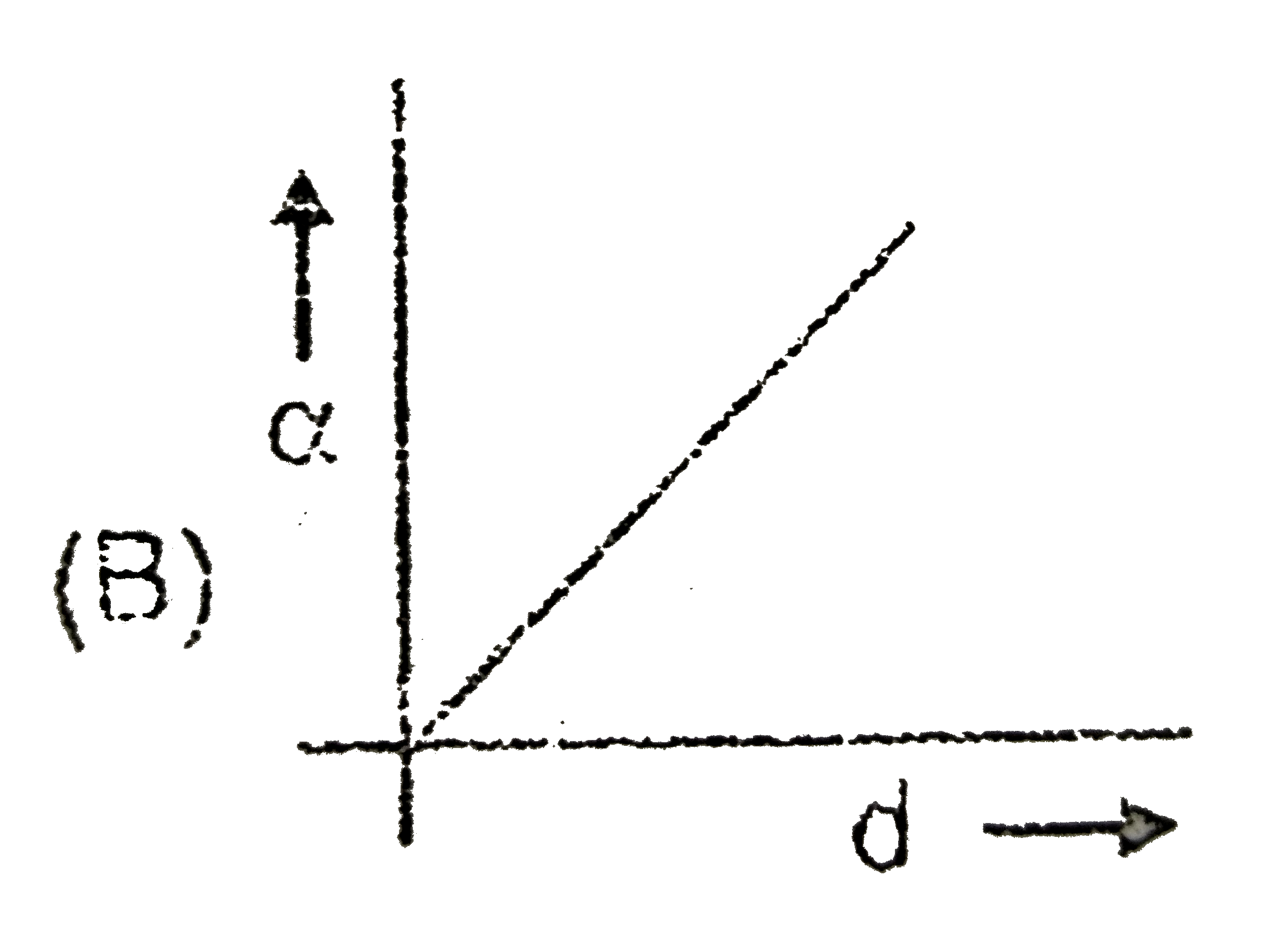
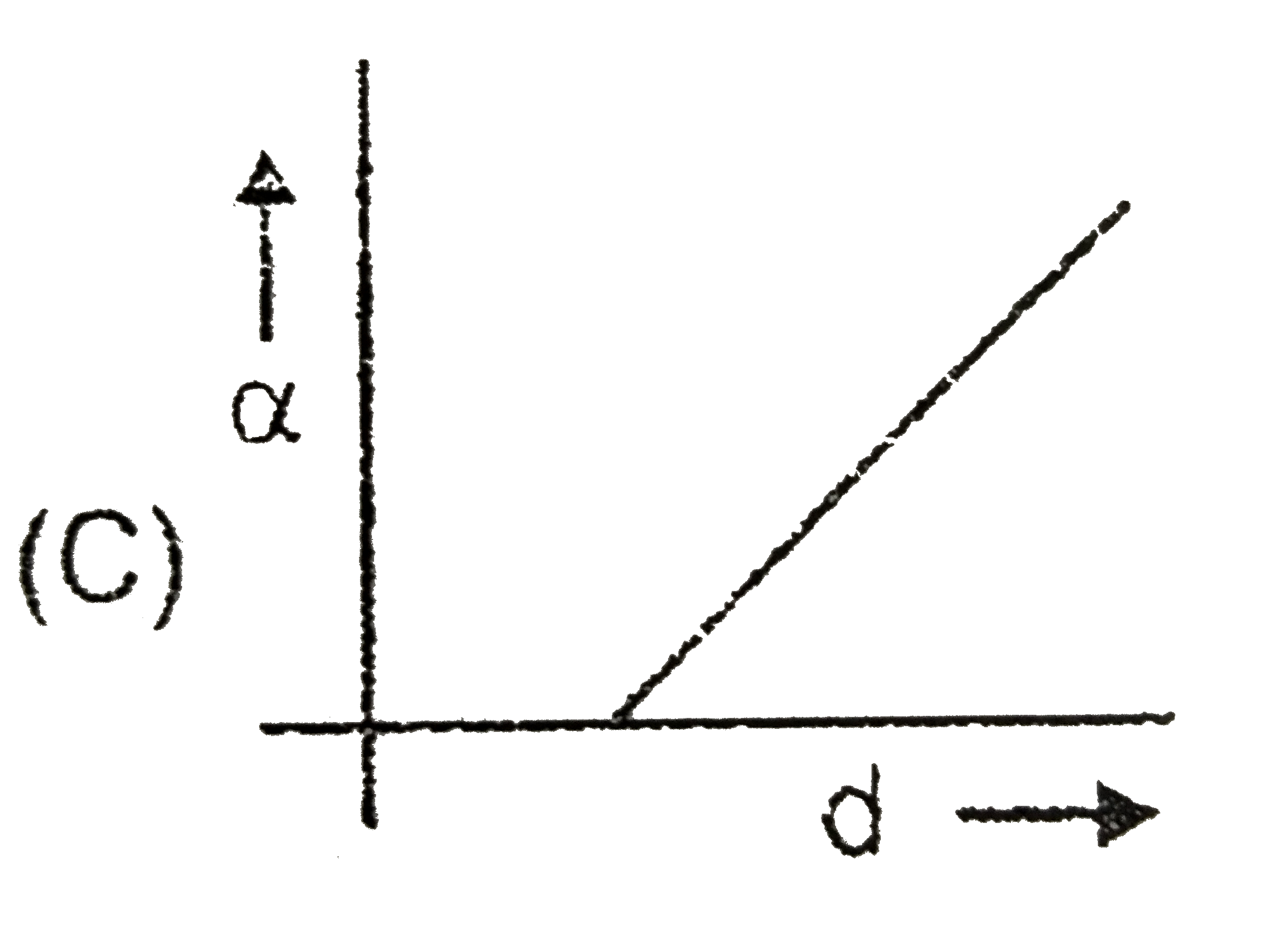
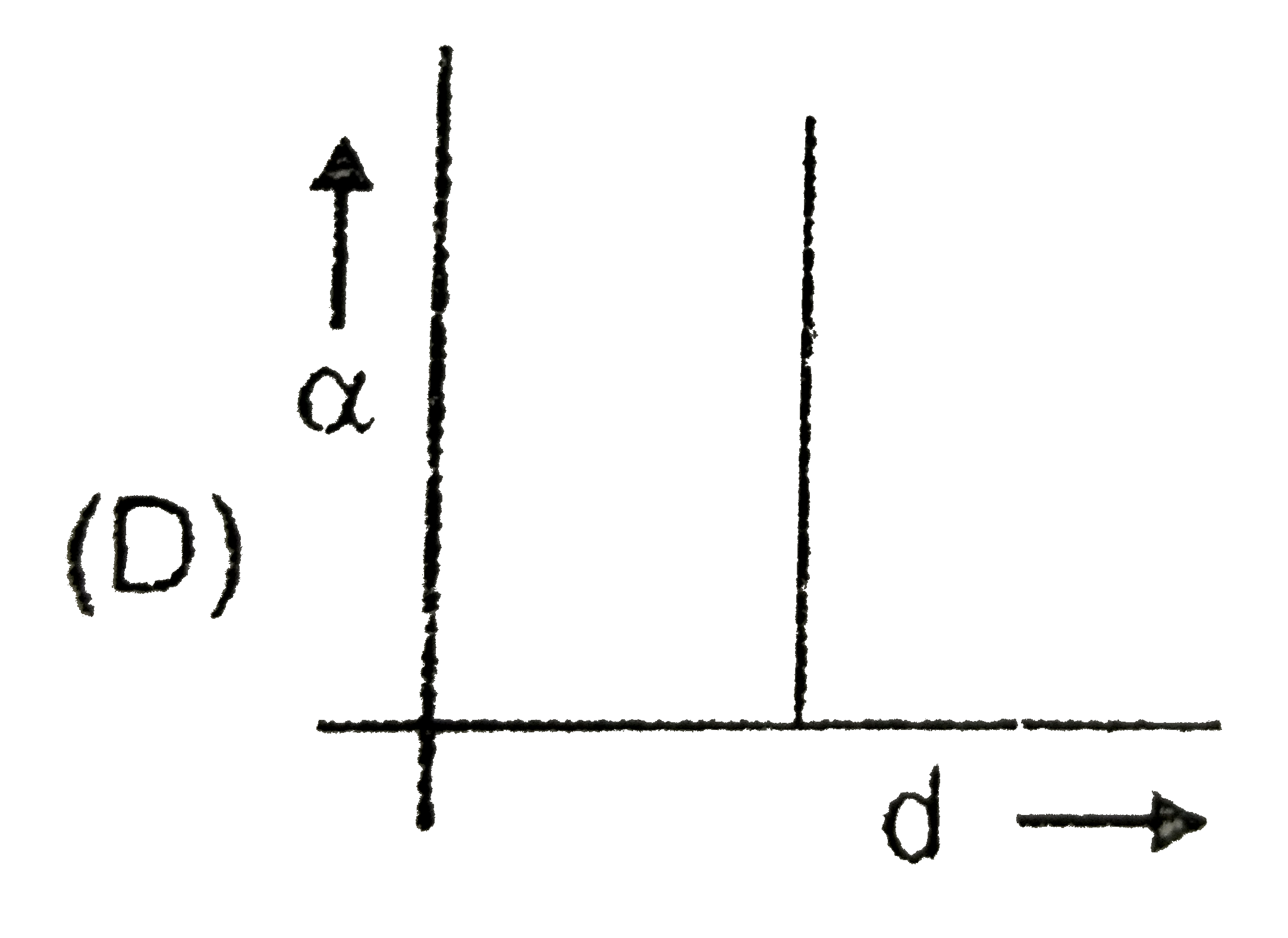
The correct Answer is:D
To solve the problem, we need to analyze the dissociation of solid carbon (C) into gaseous A and solid B, considering the dissociation fraction (α) and the density (D) of the gaseous mixture.
1. Understanding the Reaction:
The reaction is given as:
C(s)⇌2A(g)+B(s)
Here, C is in solid state, A is in gaseous state, and B is also in solid state.
2. Initial Conditions:
Initially, the container only contains solid C. Let’s denote the initial amount of C as n0.
3. Dissociation of C:
If the dissociation of C is α, then the amount of C that dissociates is αn0. Therefore, the amount of C remaining after dissociation is:
nC=n0−αn0=n0(1−α)
4. Formation of A and B:
From the stoichiometry of the reaction, for every mole of C that dissociates, 2 moles of A are produced. Thus, the moles of A produced are:
nA=2αn0
The amount of solid B formed is equal to the amount of C that dissociated:
nB=αn0
5. Total Moles in the Gaseous Mixture:
Since B is solid and does not contribute to the gas phase, the total moles in the gaseous phase is just the moles of A:
ngas=nA=2αn0
6. Density of the Gaseous Mixture:
The density (D) of the gaseous mixture is given by the formula:
D=mgasV
where mgas is the mass of the gas and V is the volume. The mass of the gas is:
mgas=nA×MA=2αn0MA
Thus, the density can be expressed as:
D=2αn0MAV
7. Conclusion on Density:
Since the reaction is carried out at constant temperature and pressure, the volume (V) can be expressed using the ideal gas law:
PV=ngasRT
Substituting ngas:
V=2αn0RTP
Now substituting V back into the density equation gives:
D=2αn0MAP2αn0RT=MAPRT
This shows that the density D is independent of α, as it remains constant regardless of the dissociation of C.
Final Answer:
The density of the gaseous mixture remains constant as α increases.
The reaction is given as:
C(s)⇌2A(g)+B(s)
Here, C is in solid state, A is in gaseous state, and B is also in solid state.
Initially, the container only contains solid C. Let’s denote the initial amount of C as n0.
If the dissociation of C is α, then the amount of C that dissociates is αn0. Therefore, the amount of C remaining after dissociation is:
nC=n0−αn0=n0(1−α)
From the stoichiometry of the reaction, for every mole of C that dissociates, 2 moles of A are produced. Thus, the moles of A produced are:
nA=2αn0
The amount of solid B formed is equal to the amount of C that dissociated:
nB=αn0
Since B is solid and does not contribute to the gas phase, the total moles in the gaseous phase is just the moles of A:
ngas=nA=2αn0
The density (D) of the gaseous mixture is given by the formula:
D=mgasV
where mgas is the mass of the gas and V is the volume. The mass of the gas is:
mgas=nA×MA=2αn0MA
Thus, the density can be expressed as:
D=2αn0MAV
Since the reaction is carried out at constant temperature and pressure, the volume (V) can be expressed using the ideal gas law:
PV=ngasRT
Substituting ngas:
V=2αn0RTP
Now substituting V back into the density equation gives:
D=2αn0MAP2αn0RT=MAPRT
This shows that the density D is independent of α, as it remains constant regardless of the dissociation of C.
The density of the gaseous mixture remains constant as α increases.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Advanced Level Problems (Part-2)(Section-2)
6 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Advanced Level Problems (Part-2)(Section-3)
6 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Advanced Level Problems (Part-1)
31 Videos
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column
1 Video
Similar Questions
At constant pressure the r.m.s. velocity c is related to density d as
View SolutionConsider the following statements :
(I)An increase in pressure (caused by decrease in volume) at equilibrium results in increase in molar concentration of each gasous substances involved.
(II)An increase in pressure (caused by decrease in volume) at equilibrium results in increase in no. of moles of each gaseous substance involved.
(III)For the reaction A(s)⇔B(g)+C(g) at constant temperature, total pressure at equilibrium (of B(g) & C(g)) is not affected by changing the volume of container.
(IV)H2O(l)⇔H2O(g) on temperature increase K of this reaction is increased.
Tick the correct statement(s)
View SolutionThere are two closed containers A and B. Container A contains PCl5 gas at 25∘C temperature and 1 bar pressure. Container B contains equilibrium mixture of gases obtained by partial decomposition of PCl5 (g) at the same temperature and pressure. Assuming that initially equal mole of PCl5 (g) at same temperature and pressure . Assuming that initially equal moles of PCl5 were taken into the containers ( before decomposition ), the gases are allowed to effuse through a pinhole in the containers, Which container will show higher rate of effusion ? Justify .
View SolutionState the S.I. and C.G.S. units of density. How are they related ?
View SolutionShow that Kp for the reaction,
2H2S(g)⇔2H2(g)+S2(g) is given by the expression
Kp=α3P(2+α)(1−α)2
where α is the degree of dissociation and P is the total equilibrium pressure. Calculate Kc of the reaction if α at 298 k and 1 atm . pressure is 0.055.
View SolutionThe equilibrium constant for the reaction 2A+2B⇔2C+2D is 200. The equilibrium constant for the reaction A+B⇔C+D, at the same temperature is ………..
View SolutionExpress the relationship between the C.G.S. and S.I. units of density.
View SolutionThe following are some state ments regarding dissociation of lime stone according to the equation CaCO3(s)⇔CaO(s)+CO2(g):ΔH = 110 kJ. The reaction is carried in a closed vessel.
A) The pressure of CO2 increases when temperature is inereased.
B) The pressure of CO2 inereases when temperature is deereased
C) The pressure of CO2 increases when amount of CaCO3 is decreased. The incorrect statements are .
View SolutionTwo solid compounds A and B dissociate into gaseous products at 20∘C as
a. A(s)⇔A'(s)+H2S(g)
b. B(s)⇔B'(g)+H2S(g)
At 20∘C pressure over excess solid A is 50 mm and that over excess solid B is 68 mm. Find:
a. The dissociation constant of A and B
b. Relative number of moles of A' and B' in the vapour phase over a mixture of the solids A and B.
c. Show that the total pressure of gas over the solid mixture would be 84.4 mm.
View SolutionTwo solid AandB are present in two different container having same volume and same temperature following equilibrium are established:
In container (1)A(s)⇔D(g)+C(g)PT=40atm at equilibrium
In container (2)B(s)⇔E(g)+F(g)PT=60atm at equilibrium
If excess of AandB are added to a third container having double the volume and at same temperature then, the total pressure of this container at equilibrium is:
View Solution
