N2O4→2NO2
In the above equation, α varies with Dd according to:
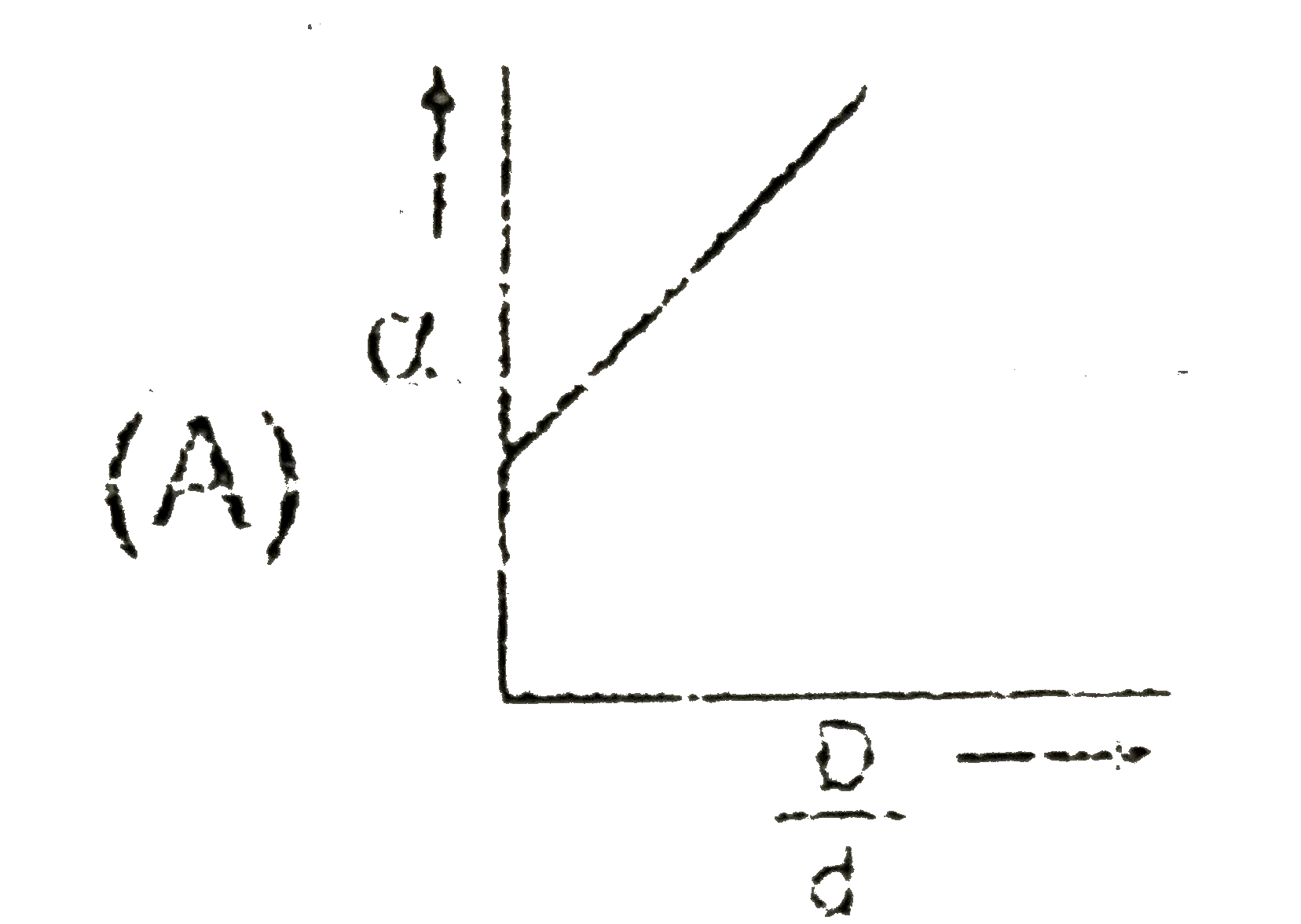


The correct Answer is:B
To solve the problem regarding the dissociation of N2O4 into 2NO2 and the relationship between the degree of dissociation (α) and the ratio of vapor densities (Dd), we can follow these steps:
1. Understand the Reaction:
The reaction is given as:
N2O4⇌2NO2
Here, one mole of N2O4 dissociates to form two moles of NO2.
2. Define the Degree of Dissociation (α):
The degree of dissociation (α) is defined as the fraction of the original substance that has dissociated. If we start with 1 mole of N2O4, then after dissociation:
- Moles of N2O4 remaining = 1−α
- Moles of NO2 formed = 2α
3. Calculate the Total Moles After Dissociation:
The total moles after dissociation will be:
Total moles=(1−α)+2α=1+α
4. Relate Vapor Density to Moles:
The vapor density (D) is related to the number of moles. The vapor density before dissociation is:
D=Vapor density before dissociation=P0
After dissociation, the vapor density (d) is given by:
d=Vapor density after dissociation=Total massTotal volume=M(1+α)V
where M is the molar mass and V is the volume.
5. Express D and d in Terms of P0:
The vapor density before dissociation is:
D=P0
The vapor density after dissociation can be expressed as:
d=P0(1+α)
6. Formulate the Ratio Dd:
Now, we can find the ratio of the vapor densities:
Dd=P0P0(1+α)=11+α
7. Rearranging the Equation:
Rearranging gives:
D=d(1+α)
This can also be expressed as:
α=1Dd−1
8. Graphical Representation:
The equation α=1Dd−1 indicates a linear relationship between α and Dd. As Dd increases, α increases, leading to a straight line graph.
Conclusion:
The graph of α versus Dd will be a straight line, confirming that the relationship is linear.
The reaction is given as:
N2O4⇌2NO2
Here, one mole of N2O4 dissociates to form two moles of NO2.
The degree of dissociation (α) is defined as the fraction of the original substance that has dissociated. If we start with 1 mole of N2O4, then after dissociation:
- Moles of N2O4 remaining = 1−α
- Moles of NO2 formed = 2α
The total moles after dissociation will be:
Total moles=(1−α)+2α=1+α
The vapor density (D) is related to the number of moles. The vapor density before dissociation is:
D=Vapor density before dissociation=P0
After dissociation, the vapor density (d) is given by:
d=Vapor density after dissociation=Total massTotal volume=M(1+α)V
where M is the molar mass and V is the volume.
The vapor density before dissociation is:
D=P0
The vapor density after dissociation can be expressed as:
d=P0(1+α)
Now, we can find the ratio of the vapor densities:
Dd=P0P0(1+α)=11+α
Rearranging gives:
D=d(1+α)
This can also be expressed as:
α=1Dd−1
The equation α=1Dd−1 indicates a linear relationship between α and Dd. As Dd increases, α increases, leading to a straight line graph.
The graph of α versus Dd will be a straight line, confirming that the relationship is linear.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBook:RESONANCE ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-1)
Explore 28 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCE ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-2 (Part-2)
Explore 22 Videos
- CHEMICAL EQUILIBRIUMBook:RESONANCE ENGLISHChapter:CHEMICAL EQUILIBRIUMExercise:Exercise-1 (Part-1)
Explore 38 Videos
- CHEMICAL BONDINGBook:RESONANCE ENGLISHChapter:CHEMICAL BONDINGExercise:ORGANIC CHEMISTRY(Fundamental Concept )
Explore 6 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Book:RESONANCE ENGLISHChapter:D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS Exercise:Match the column
Explore 1 Video
Similar Questions
The equation α=D−d(n−1)d is correctly matched for :
View Solution2CO(g)+O2(g)→2CO2(g)+X KJ In the above equation X KJ refers to :
View SolutionConsider the decomposition of N2O5 as N2O5→2NO2+12O2 The rate of reaction is given by −d[N2O5]dt=12d[NO2]dt=2d[O2]dt=k1[N2O5] Therefore,−d[N2O5]dt=k1[N2O5] ,
+d[NO2]dt=2k1[N2O5]=k′1[N2O5],d[O2]dt=12k1[N2O5]=k''1[N2O5] Choose the correct option.
View SolutionConsider the reactions 12N2+O2⇔NO2K1
2NO2⇔N2O4K2
Using above equations , write down expression for K of the following reaction N2O4⇔N2+2O2K
View SolutionAt the equilibrium of the reaction ,
N2O4(g)⇒2NO2(g), the observed molar mass of N2O4 is 77.70 g . The percentage dissociation of N2O4 is :-
View SolutionFor the reaction : 2N2O5→4NO2+O2, the rate of reaction in terms of O2 is d[O2]/dt. In terms of N2O5, it will be :
View SolutionFe2O3+2Al→Al2O3+2Fe
The above reaction is an example of a
View SolutionConsider the reaction,
NO2→12N2+O2,K1,N2O4→2NO2,K2 Give the equilibrium constant for the formation of N2O4fromN2andO2.
View SolutionIn the dissociation of N2O4 into NO2,(1+α) values with the vapour densities ratio (Dd) is given by: [α degree of dissociation, D-vapour density before dissociation, d-vapour density after dissociation]
View SolutionN2+H2→[X](g)CO2,Pressure−−−−−−−→[Y]Heat−−→[Z]+H2O In the above sequence of reaction, [Y] and [Z] are respectively.
View Solution