One mole of ideal monatomic gas was taken through isochoric heating from 100 K to 1000 K. Calculate ΔSsystem,Δsurr and ΔStotal in
(i) When the process carried out reversibly (ii) When the process carried out irreversibly (one step)
The correct Answer is:(i) Rev. Process ΔSsystem=32RIn10;ΔSsurr=−32R∈10 ΔStotal=0
Irr. Process ΔSsystem=32RIn10;ΔSsurr=−32R(0.9);ΔStotal=32R(1.403)
To solve the problem, we need to calculate the change in entropy for the system, the surroundings, and the total entropy for both reversible and irreversible processes during isochoric heating of one mole of an ideal monatomic gas from 100 K to 1000 K.
1. Calculate the change in entropy of the system (ΔSsystem):
ΔSsystem=∫T2T1dQT
Since the process is isochoric, dQ=nCVdT:
ΔSsystem=∫T2T1nCVdTT
Substituting CV=32R:
ΔSsystem=n⋅32R∫T2T1dTT
=32Rln(T2T1)
=32Rln(1000100)=32Rln(10)
2. Calculate the change in entropy of the surroundings (ΔSsurr):
ΔSsurr=−dQTsurr
For isochoric heating, we can use the final temperature of the system as the temperature of the surroundings:
dQ=nCV(T2−T1)=n⋅32R(1000−100)
=32R(900)
Thus,
ΔSsurr=−32R(900)1000
=−32R⋅0.9=−2720R
3. Calculate the total change in entropy (ΔStotal):
ΔStotal=ΔSsystem+ΔSsurr
=32Rln(10)−2720R
(ii) Irreversible Process
1. Calculate the change in entropy of the system (ΔSsystem):
The change in entropy for the system remains the same as in the reversible case:
ΔSsystem=32Rln(10)
2. Calculate the change in entropy of the surroundings (ΔSsurr):
The calculation for the surroundings remains the same:
ΔSsurr=−2720R
3. Calculate the total change in entropy (ΔStotal):
The total change in entropy is still:
ΔStotal=ΔSsystem+ΔSsurr
=32Rln(10)−2720R
Final Results
- ΔSsystem=32Rln(10)
- ΔSsurr=−2720R
- ΔStotal=32Rln(10)−2720R
ΔSsystem=∫T2T1dQT
Since the process is isochoric, dQ=nCVdT:
ΔSsystem=∫T2T1nCVdTT
Substituting CV=32R:
ΔSsystem=n⋅32R∫T2T1dTT
=32Rln(T2T1)
=32Rln(1000100)=32Rln(10)
ΔSsurr=−dQTsurr
For isochoric heating, we can use the final temperature of the system as the temperature of the surroundings:
dQ=nCV(T2−T1)=n⋅32R(1000−100)
=32R(900)
Thus,
ΔSsurr=−32R(900)1000
=−32R⋅0.9=−2720R
ΔStotal=ΔSsystem+ΔSsurr
=32Rln(10)−2720R
The change in entropy for the system remains the same as in the reversible case:
ΔSsystem=32Rln(10)
The calculation for the surroundings remains the same:
ΔSsurr=−2720R
The total change in entropy is still:
ΔStotal=ΔSsystem+ΔSsurr
=32Rln(10)−2720R
- ΔSsystem=32Rln(10)
- ΔSsurr=−2720R
- ΔStotal=32Rln(10)−2720R
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 Part-3 :(Subjective questions)Section C
6 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 Part-3 :(Only one option correct type) section A
8 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 Part-3 :(Subjective questions)Section A
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
One mole of Ideal monatomic gas taken through Isochoric heating for 100K to 1000K then correct Match is
View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
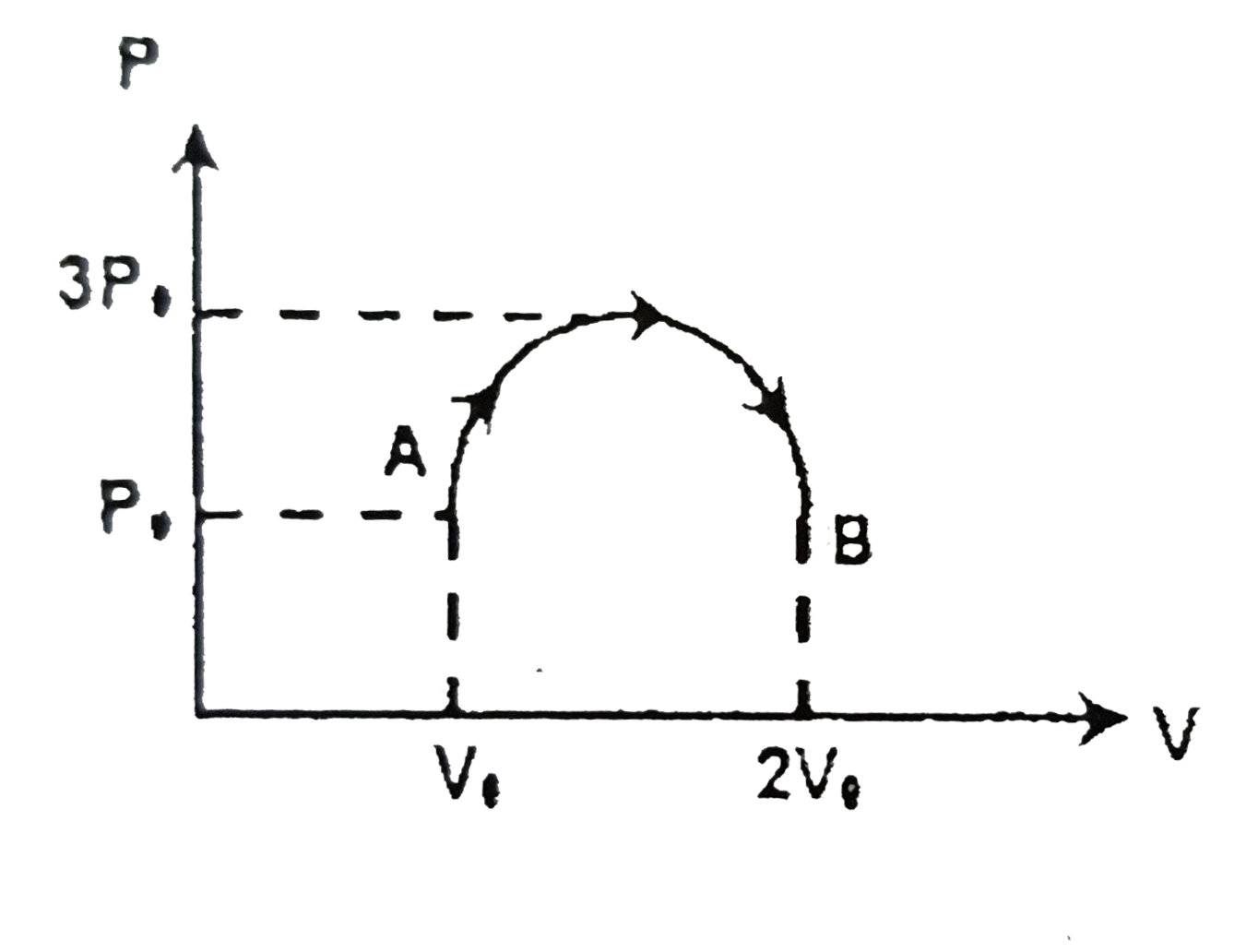
View SolutionOne mole of ideal monoatmic gas is carried throught the reversible cyclic process as shown in figure. Calculate net heat absorbed by the gas in the path BC
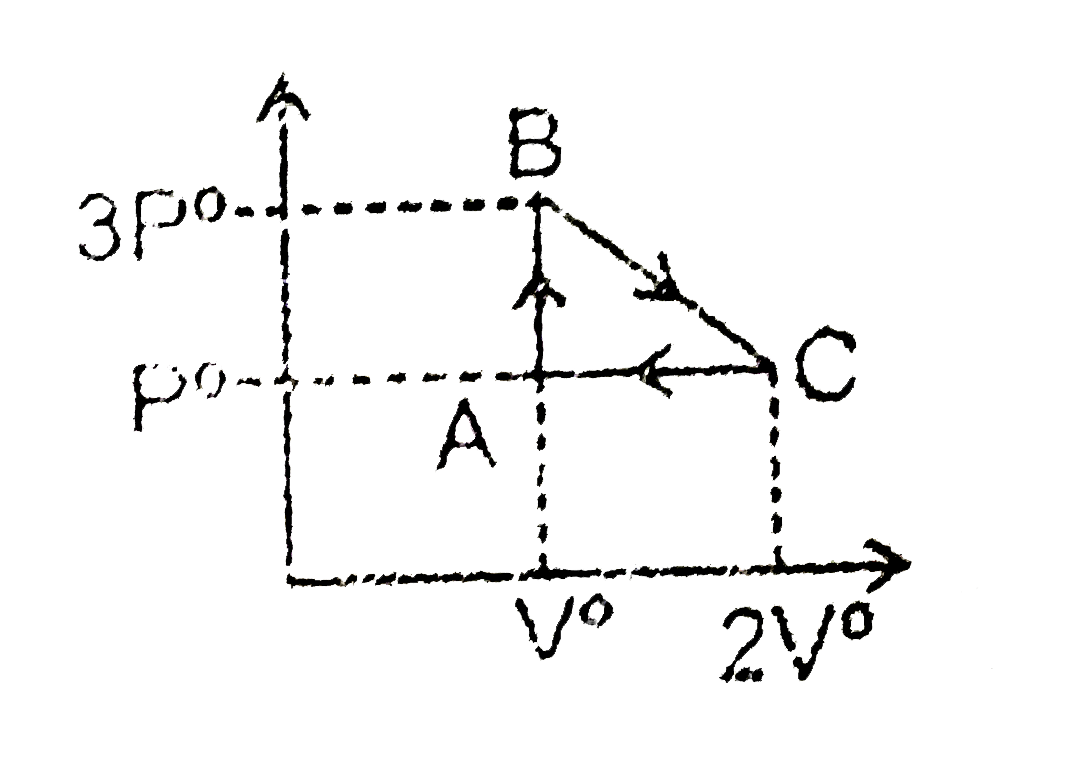
View SolutionOne mole of ideal monatomic gas is carried through the reversible cyclic process as shown in figure. Calculate the max temperature attained by the gas during the cycle.
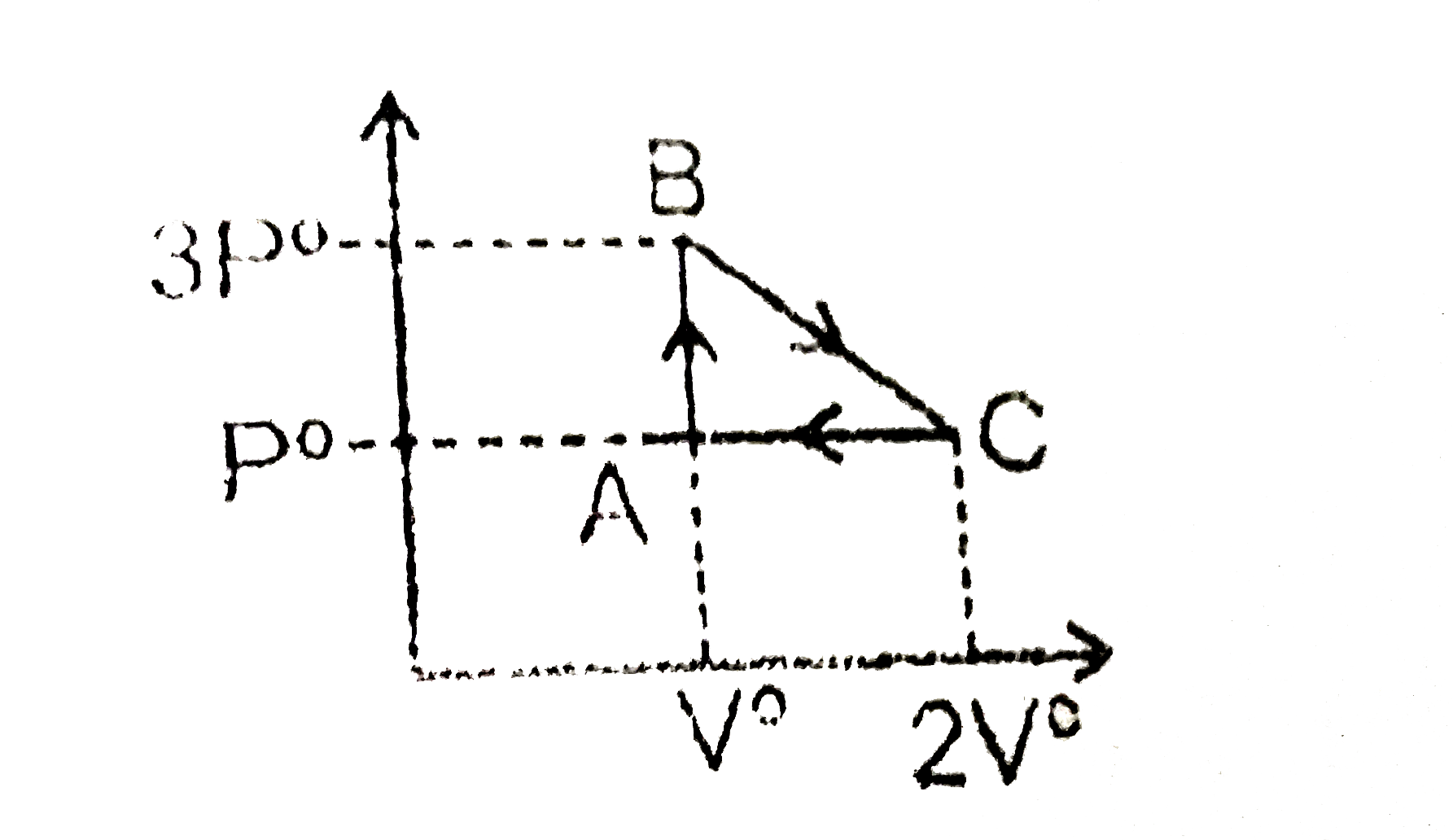
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionThe entropy change when two moles of ideal monatomic gas is heated from 200to300∘C reversibly and isochorically ?
View SolutionOne mole of an ideal gas is expanded isothermally at 300 K until its volume is tripled . Find the values of ΔSsys under the condition.
View SolutionOne moles of an ideal gas which CV=3/2R is heated at a constant pressure of 1atm from 25∘C to 100∘C. Calculate ΔU,ΔH and the entropy change during the process.
View Solution
