Following graph shows a single stange expansion process, then workdone by the system is
−9104J
−202.6J
−506J
−101.3J
To solve the problem of calculating the work done by the system during a single-stage expansion process, we can follow these steps:
1. Identify the Process:
- The problem describes a single-stage expansion process where the gas expands against a constant pressure of 1 atm.
2. Understand the Work Done Formula:
- The work done (W) by the system during an expansion at constant pressure is given by the formula:
W=−PΔV
- Where P is the pressure (in atm) and ΔV is the change in volume (in liters).
3. Determine the Change in Volume (ΔV):
- From the graph, we can see that the initial volume (V1) is 0 liters and the final volume (V2) is 4 liters.
- Therefore, the change in volume is:
ΔV=V2−V1=4liters−0liters=4liters
4. Substitute Values into the Work Done Formula:
- Now, substituting the values into the work done formula:
W=−PΔV=−1atm×4liters=−4liter atm
5. Convert Work Done to Joules:
- We know that 1 liter atm is approximately equal to 100 Joules. Therefore:
W=−4liter atm×100J/liter atm=−400J
6. Conclusion:
- The work done by the system during the single-stage expansion process is:
W=−400J
Final Answer:
The work done by the system is −400J.
---
- The problem describes a single-stage expansion process where the gas expands against a constant pressure of 1 atm.
- The work done (W) by the system during an expansion at constant pressure is given by the formula:
W=−PΔV
- Where P is the pressure (in atm) and ΔV is the change in volume (in liters).
- From the graph, we can see that the initial volume (V1) is 0 liters and the final volume (V2) is 4 liters.
- Therefore, the change in volume is:
ΔV=V2−V1=4liters−0liters=4liters
- Now, substituting the values into the work done formula:
W=−PΔV=−1atm×4liters=−4liter atm
- We know that 1 liter atm is approximately equal to 100 Joules. Therefore:
W=−4liter atm×100J/liter atm=−400J
- The work done by the system during the single-stage expansion process is:
W=−400J
The work done by the system is −400J.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - A-1
1 Video
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - A-2
1 Video
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 part-III Advanced level Solutions (STAGE-II)
38 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Knowledge Check
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)Which of the following graphs shows a stong positive association between x and y?
A B
B C
C D
D
For an isothermal reversible expansion process, the value of q can be calculated by the expressin
Aq=2.303nRTlog.V2V1Bq=−2.303nRTlog.V2V1Cq=−2.303nRTlog.V1V2Dq=−PexpnRTlog.V1V2
in a reversible adiabatic expansion, entropy of the system
View SolutionIn a spontaneous process the system undergoes
View SolutionSelect the correct set of statement/s:
I. Work done by the surrounding in case of infinite stage expansion is more than single stage expansion
II. Irreversible work is always greater than reversible work.
III. On an ideal gas in case of single stage expansion and compression system as well as surrounding are restored back to their original states
IV. If gas is in thermodynamic equilibrium is taken from A to state B, by four successive single stage expansions. Then we can plot 4 points on the P-V indicator diagram.
View SolutionThe following graphs shows two isothermal process for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at temperatures T1 and T2?
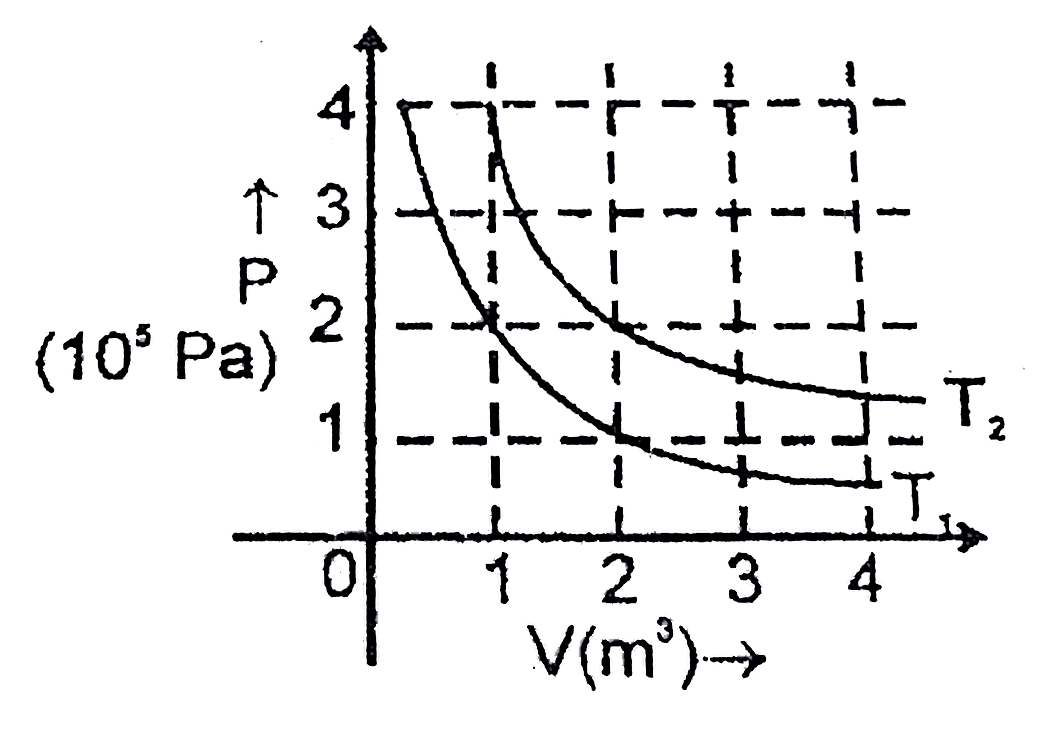
View SolutionThe state of a mole of an ideal gas changed from state A at pressure 2P and volume V follows four different processes and finally returns to initial state A reversibly as shown below in the graph. By interpreting the graph, answer the following questions.
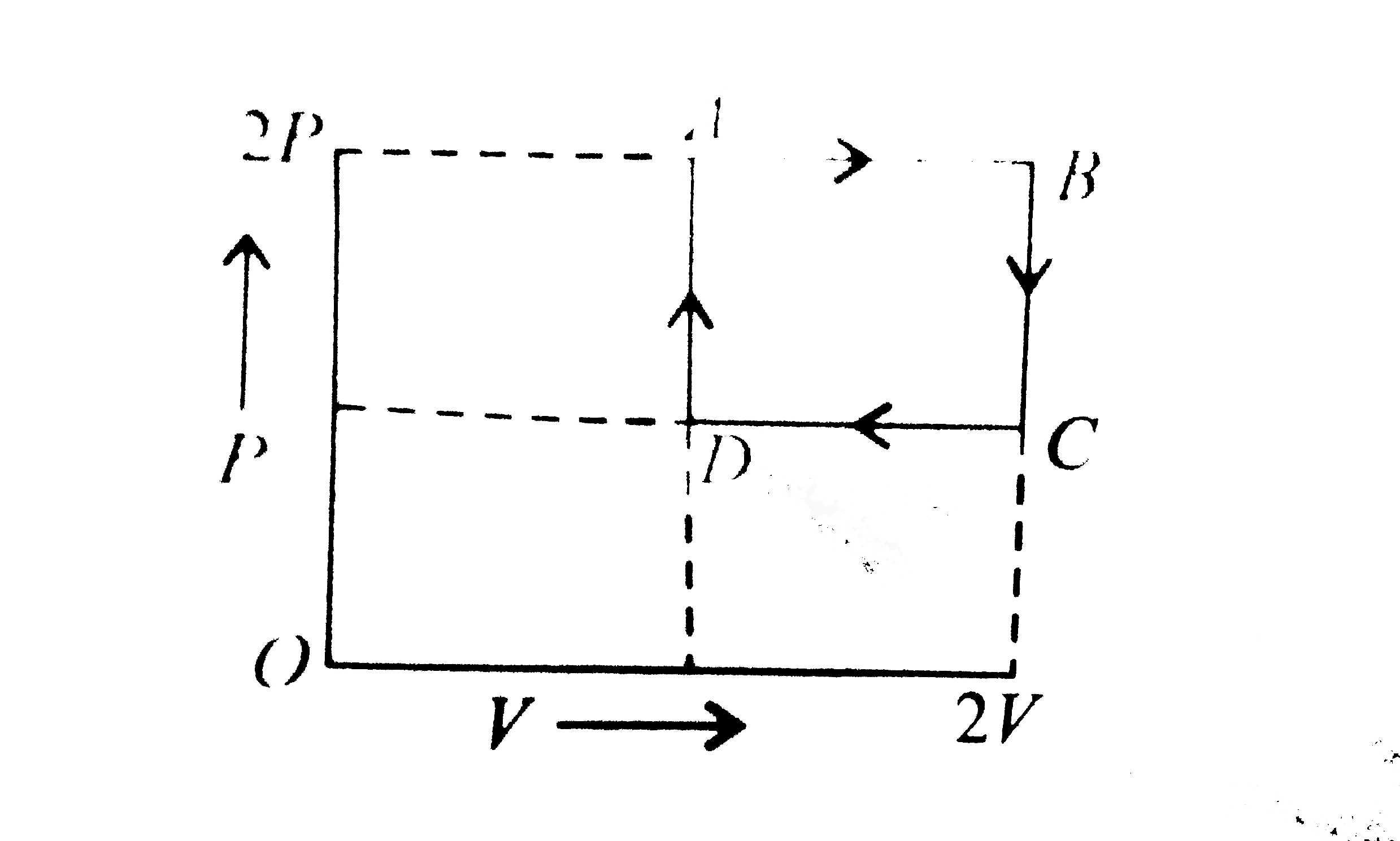
What would be the heat obsorbed by the system in this cyclic process?
View Solution

