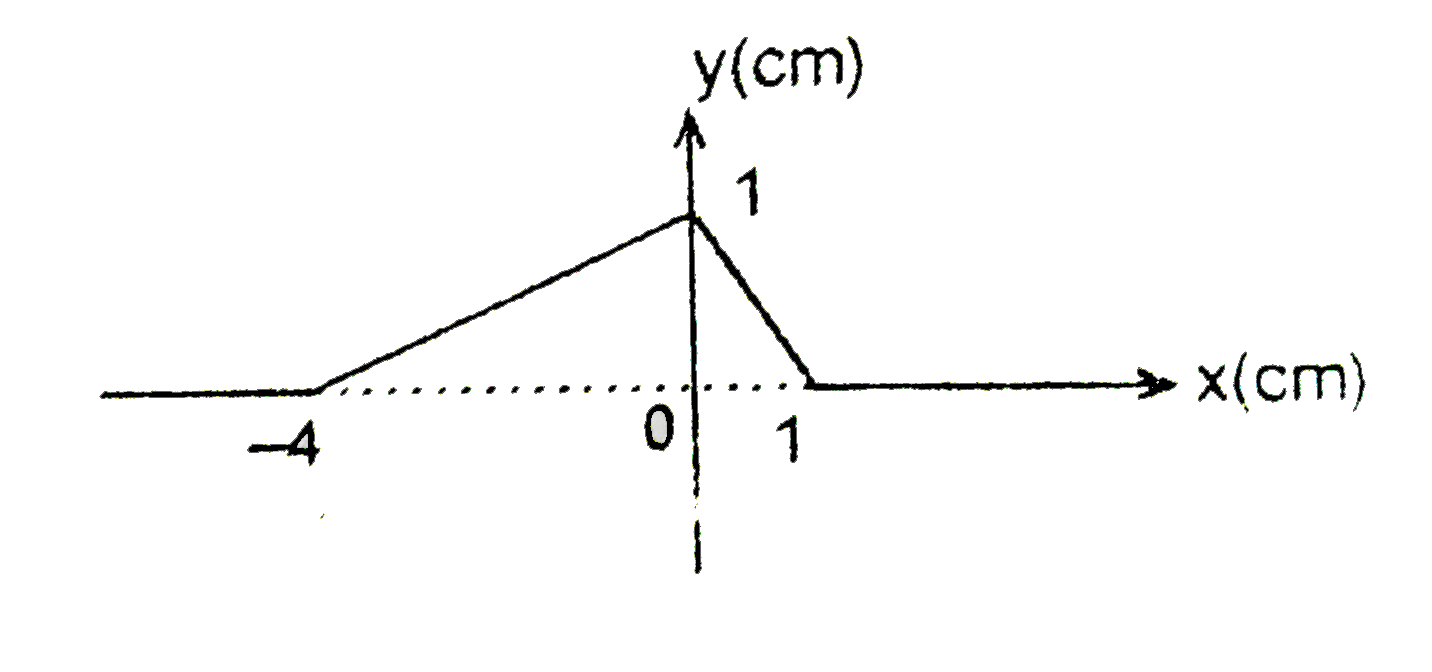
A pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪
⎪⎨⎪
⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
the shape of the string is drawn at t=0 and lthe area of the pulse elclosed by the string and the x−string is measured. It will be equal to
2cm2
2.5cm2
4cm2
5cm2
The correct Answer is:B
Shape of the pulse at t=0
That is a triangular pulse Area of the pulse
=12[(4×1)+(1×1)]
=52cm2
Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART II
Explore 7 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 3 PART I
Explore 19 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 2 PART III
Explore 15 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 3 PART II
Explore 7 Videos
Similar Questions
A pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The vertical displacement of the particle of the string at x=7cm and t=0.01s will be
View SolutionA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The transverse velocity of the particle at x=13cm and t=0.015s will be
View SolutionA pulse is started at a time t=0 along the +xdirection on a long, taut string. The shape of the pulse at t=0 is given by function f(x) with
here f and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N.
The transverse velocity of the particle at x=13cm and t=0.015s will be
View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,
View SolutionA pulse moving to the right along the x-axis is represented by the wave function
where x and y are measured in cedntimetres and t is measured in seconds. Find expression for the wave function at t=0,t=1.0s,andt=2.0s and plote the shape of pulse at these lines.
View SolutionA wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
View SolutionA particle of mass m is moving along a trajectory given by
x=x0+acosω1t
y=y0+bsinω2t
The torque, acting on the particle about the origin, at t=0 is:
View SolutionFind the value of the products: (x+2y)(x−2y)at x=1, y=0
View Solution

