A circuit is set up by connecting L=100mH, C=5μF and R=100Ω in series. An alternating emf of 150 sqrt(2)V,(500)/(pi) Hz is applied across this series combination. Which of the following is correct:
the impedance of the circuit is 141.4Ω
the average power dissipated across resistance 225W
the average power dissipated across inductor is zero.
the average power dissipated across capacitor is zero
The correct Answer is:A,B,C,D
To solve the problem step by step, we will analyze the given circuit parameters and calculate the required values.
Step 1: Identify the given values
- Inductance (L) = 100 mH = 100 × 10^-3 H
- Capacitance (C) = 5 µF = 5 × 10^-6 F
- Resistance (R) = 100 Ω
- Alternating emf (V) = 150√2 V
- Frequency (f) = (500/π) Hz
Step 2: Calculate the angular frequency (ω)
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π(500π)=1000rad/s
Step 3: Calculate the inductive reactance (X_L)
The inductive reactance (X_L) is given by:
XL=ωL
Substituting the values:
XL=1000×(100×10−3)=100Ω
Step 4: Calculate the capacitive reactance (X_C)
The capacitive reactance (X_C) is given by:
XC=1ωC
Substituting the values:
XC=11000×(5×10−6)=10.000005=200Ω
Step 5: Calculate the impedance (Z)
The total impedance (Z) in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√1002+(100−200)2=√10000+(−100)2=√10000+10000=√20000=141.42Ω
Step 6: Calculate the current (I)
The RMS current (I) can be calculated using Ohm's law:
I=VrmsZ
Substituting the values:
I=150√2141.42≈1.06A
Step 7: Calculate the average power (P) dissipated across the resistor (R)
The average power (P) dissipated across the resistor is given by:
P=I2R
Substituting the values:
P=(1.06)2×100≈112.36W
Step 8: Conclusion
- The average power dissipated across the resistor is approximately 112.36 W.
- The average power dissipated across the inductor and capacitor is 0 W because the phase difference between voltage and current in inductors and capacitors is 90 degrees.
Summary of Results
1. Inductive Reactance (X_L) = 100 Ω
2. Capacitive Reactance (X_C) = 200 Ω
3. Impedance (Z) = 141.42 Ω
4. Average Power across Resistor (P) ≈ 112.36 W
5. Average Power across Inductor = 0 W
6. Average Power across Capacitor = 0 W
- Inductance (L) = 100 mH = 100 × 10^-3 H
- Capacitance (C) = 5 µF = 5 × 10^-6 F
- Resistance (R) = 100 Ω
- Alternating emf (V) = 150√2 V
- Frequency (f) = (500/π) Hz
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π(500π)=1000rad/s
The inductive reactance (X_L) is given by:
XL=ωL
Substituting the values:
XL=1000×(100×10−3)=100Ω
The capacitive reactance (X_C) is given by:
XC=1ωC
Substituting the values:
XC=11000×(5×10−6)=10.000005=200Ω
The total impedance (Z) in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√1002+(100−200)2=√10000+(−100)2=√10000+10000=√20000=141.42Ω
The RMS current (I) can be calculated using Ohm's law:
I=VrmsZ
Substituting the values:
I=150√2141.42≈1.06A
The average power (P) dissipated across the resistor is given by:
P=I2R
Substituting the values:
P=(1.06)2×100≈112.36W
- The average power dissipated across the resistor is approximately 112.36 W.
- The average power dissipated across the inductor and capacitor is 0 W because the phase difference between voltage and current in inductors and capacitors is 90 degrees.
1. Inductive Reactance (X_L) = 100 Ω
2. Capacitive Reactance (X_C) = 200 Ω
3. Impedance (Z) = 141.42 Ω
4. Average Power across Resistor (P) ≈ 112.36 W
5. Average Power across Inductor = 0 W
6. Average Power across Capacitor = 0 W
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-4
Explore 11 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -3 Part-1
Explore 7 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-2
Explore 6 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
A voltage source V=V0sin(100t) is connected to a black box in which there can be either one element out of L,C,R or any two of them connected in series.
At steady state, the variation of current in the circuit and the source voltage are plotted together with time.using an oscilloscope, as shown
The element (s) present in black box is/are:

View SolutionAn AC voltage source of variable angular frequency (ω) and fixed amplitude V0 is connected in series with a capacitance C and an electric bulb of resistance R (inductance zero). When (ω) is increased
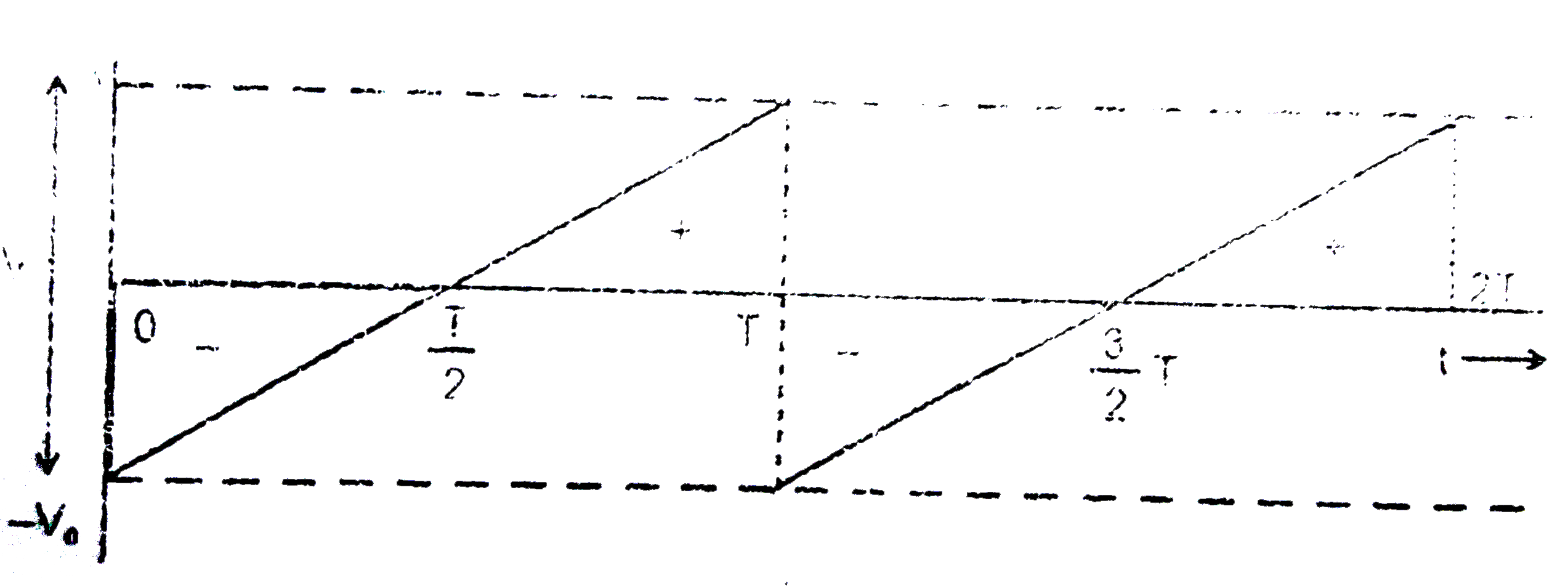
View SolutionThe rms value of the saw-tooth voltage of peak value V0 from t=0 to t=2T as shown in figure is V0√x.Find the value of x.
View SolutionA small particle of mass m moves in such a way that the potential energy U=12m2ω2r2, where ω is a constant and r is the distance of the particle from the origin. Assuming Bohr model of quantization of angular momentum and circular orbits, show that radius of the nth allowed orbit is proportional to √n.
View SolutionA circuit is set up by connecting L=100mH, C =5muF and R =100Omega in series. An alternating emf of 150 sqrt(2)V,(500)/(pi) Hz is applied across this series combination. Which of the following is correct:
View SolutionIn an L C R circuit having L = 8 H, C = 0 5muF and R=100Omega in series, the resonance frequency in rad/s is
View SolutionAn inductance of 100 mH and a resistance of 100 Ω are connected in series and an alternating emf of peak value 100 V, 50 Hz is applied across the combination. The power factor of the circuit is
View SolutionIn inductance of (4//pi) H and the resistor R, are connected in series and an alternating emf of frequency 50 Hz is applied across combination. If phase difference between applied emf and current is 45^(@) then the value of R is
View SolutionIn an LCR series combination, R=400 Omega L=100mH and C=1muF . This combination is connected to a 25sin2000t volt source. Find dissipated power in the circuit.
View SolutionA circuit is set up connecting L=100 mH, C= 5muF and R= 100Omega is series, An alternating emf of (150sqrt2)vol t,500/piHz is applied across this series combination. Calculate the impedance of the circuit. What is the average power dissipated in the resistor
View SolutionA circuit is set up connecting L=100 mH, C=5μF and R=100Ω is series, An alternating emf of (150√2)volt,500πHz is applied across this series combination. What is the average power dissipated in the capacitor
View SolutionA circuit is set up connecting L=100 mH, C= 5muF and R= 100Omega is series, An alternating emf of (150sqrt2)vol t,500/piHz is applied across this series combination. Calculate the impedance of the circuit. What is the average power dissipated in the inductor?
View SolutionFor an alternating current of frequency (500 )/(pi) Hz in L-C-R series circuit with L = 1H, C = 1muF, R = 100 Omega , impedance is-
View SolutionIn an RC series circuit connected across and AC source of 150 V 70 Hz, the value of R is 820 Omega and voltage across it is 100V. Calculate the voltage drop across capacitor connected in series.
View SolutionAn LCR series circuit with L = 80 mH, C = 60 muF and R= 100Omega is connected to a 230 V, 50 Hz AC source. Calculate the p.d. across L,C and R
View SolutionA 100 V AC source of frequency 500 Hz is connected to LCR circuit with L=8.1mH, C=12.5μF and R=100Ω, all connected in series. Find the potential (in volt) across the resistance.
View Solution

