When a voltage vS=200√2sin(ωt+15∘) is applied to an AC circuit the current in the circuit is found to be i=2sin(ωt+π/4) then average power concumed in the circuit is
(A)200 watt , (B)400√2 watt , (C )100√6 watt , (D)200√2 watt
To find the average power consumed in the circuit, we will follow these steps:
Step 1: Identify the peak voltage and peak current
The voltage is given as:
vS=200√2sin(ωt+15∘)
From this, we can identify the peak voltage:
Vmax=200√2volts
The current is given as:
i=2sin(ωt+π4)
From this, we can identify the peak current:
Imax=2amperes
Step 2: Determine the phase difference
The phase angle of the voltage is 15∘ and the phase angle of the current is π4 (which is 45∘). The phase difference ϕ between the voltage and current is:
ϕ=Phase of current−Phase of voltage=45∘−15∘=30∘
Step 3: Calculate the average power
The average power consumed in an AC circuit can be calculated using the formula:
Paverage=12VmaxImaxcos(ϕ)
Substituting the values we have:
Paverage=12×200√2×2×cos(30∘)
Step 4: Calculate cos(30∘)
We know that:
cos(30∘)=√32
Step 5: Substitute and simplify
Now substituting cos(30∘):
Paverage=12×200√2×2×√32
Paverage=200√2×√32
Paverage=100√6
Conclusion
Thus, the average power consumed in the circuit is:
Paverage=100√6watts
Final Answer
The correct option is (C) 100√6 watts.
---
The voltage is given as:
vS=200√2sin(ωt+15∘)
From this, we can identify the peak voltage:
Vmax=200√2volts
i=2sin(ωt+π4)
From this, we can identify the peak current:
Imax=2amperes
The phase angle of the voltage is 15∘ and the phase angle of the current is π4 (which is 45∘). The phase difference ϕ between the voltage and current is:
ϕ=Phase of current−Phase of voltage=45∘−15∘=30∘
The average power consumed in an AC circuit can be calculated using the formula:
Paverage=12VmaxImaxcos(ϕ)
Substituting the values we have:
Paverage=12×200√2×2×cos(30∘)
We know that:
cos(30∘)=√32
Now substituting cos(30∘):
Paverage=12×200√2×2×√32
Paverage=200√2×√32
Paverage=100√6
Thus, the average power consumed in the circuit is:
Paverage=100√6watts
The correct option is (C) 100√6 watts.
Similar Questions
When a voltage Vs=200√2sin(100t)V is applied to an ac circuit the current in the circuit is found to be i=2sin[ωt+(π/4)]A. Find the average power consumed in the circuit.
View SolutionWhen a voltage Vs=200√2sin(100t)V is applied to an ac circuit the current in the circuit is found to be i=2sin[ωt+(π/4)]A. Find the average power consumed in the circuit.
View SolutionWhen an alternating emf e=310sin(100πt)V is applied to a series LCR circuit, current flowing through it is i=5sin(100πt+π/3)A.
Calculate the average power consumed by the circuit.View SolutionVoltage input in a circuit is V = 300 sin(ωt) with current = 100 cos(ωt) . Average power loss in the circuit is
View SolutionVoltage applied to an AC circuit and current flowing in it is given by
V=200√2sin(ωt+π4) and i=−√2cos(ωt+π4)
Then, power consumed in the circuited will beView SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
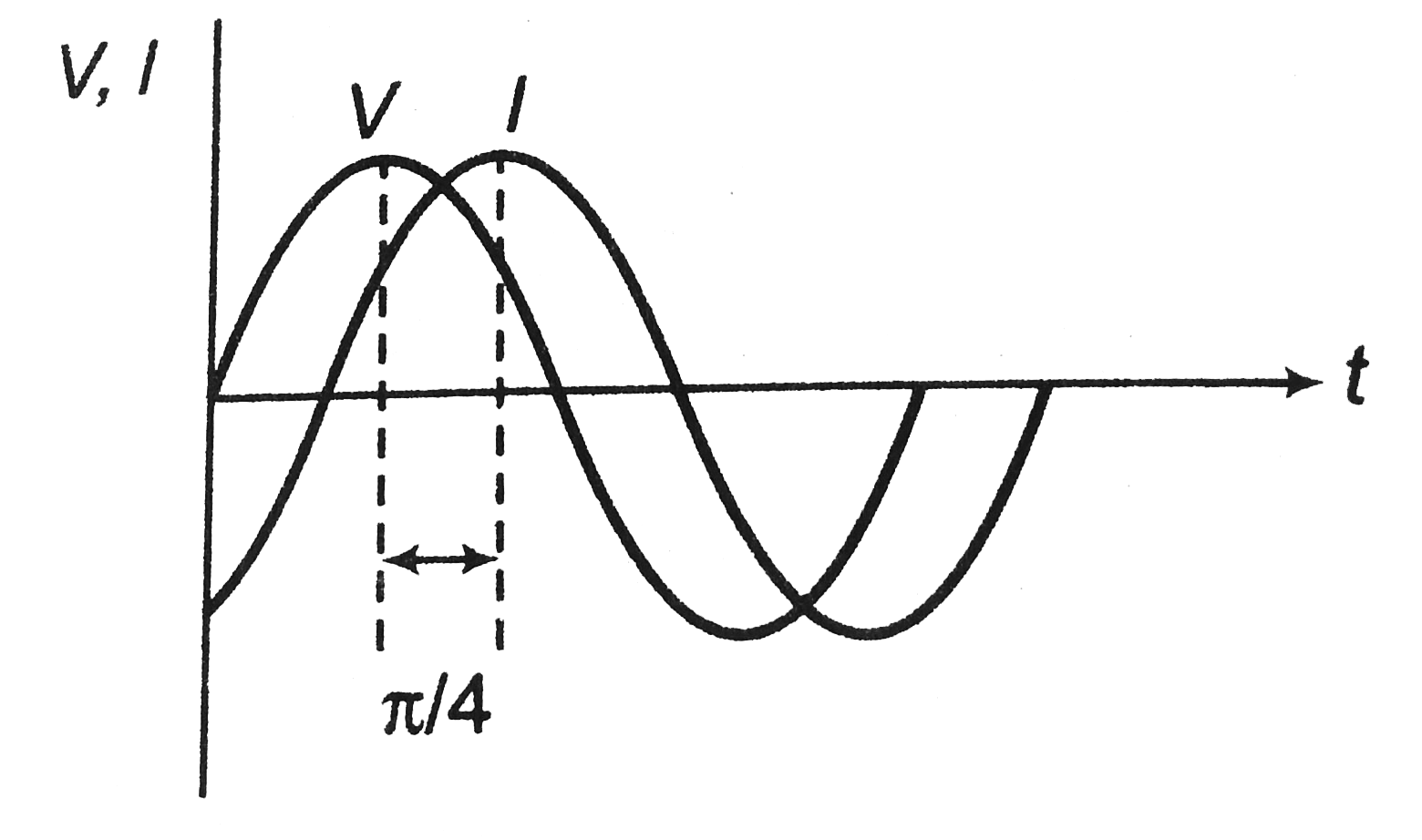 .View Solution
.View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .View Solution
.View SolutionEmf applied and current in an A.C. circuit are E=10√2sinωt volt and l=5√2cosωt ampere respectively. Average power loss in the circuit is
View SolutionThe instantaneous current in an AC circuit is l = √2sin(50 t + π / 4 ) . The rms value of current is
View SolutionIn an AC circuit, the current is given by i=5sin(100t−π2) and the AC potential is V=200sin(100t)volt. Then the power consumption is
View Solution
